题目内容
用配方法证明:x2-4x+
>0.
| 9 |
| 2 |
考点:配方法的应用,非负数的性质:偶次方
专题:证明题
分析:先利用配方法得到:x2-4x+
=(x-2)2+
,然后根据非负数的性质进行证明.
| 9 |
| 2 |
| 1 |
| 2 |
解答:证明:x2-4x+
=(x-2)2+
,
∵(x-2)2≥0,
∴(x-2)2+
>0.
故x2-4x+
>0.
| 9 |
| 2 |
| 1 |
| 2 |
∵(x-2)2≥0,
∴(x-2)2+
| 1 |
| 2 |
故x2-4x+
| 9 |
| 2 |
点评:本题考查了配方法:配方法的理论依据是公式a2±2ab+b2=(a±b)2.也考查了非负数的性质.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
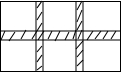 如图是宽为30m,长为44m的矩形草皮,要修筑同样宽的三条水渠(两条纵向,一条横向,且互相垂直),把草皮分成六块,要使余下草皮的面积为1120m2,求水渠宽为多少米?
如图是宽为30m,长为44m的矩形草皮,要修筑同样宽的三条水渠(两条纵向,一条横向,且互相垂直),把草皮分成六块,要使余下草皮的面积为1120m2,求水渠宽为多少米?
 如图,过A点画与直线BC垂直的线段,A点到BC的距离是线段
如图,过A点画与直线BC垂直的线段,A点到BC的距离是线段