题目内容
8.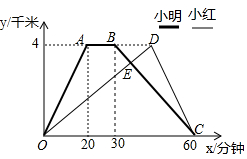 小明和小红同时从学校出发骑自行车到公园后返回,他们与学校的距离y(千米)和离开学校的时间x(分钟)之间的关系如图.
小明和小红同时从学校出发骑自行车到公园后返回,他们与学校的距离y(千米)和离开学校的时间x(分钟)之间的关系如图.请根据图象回答:
(1)如果小明两次经过途中某一地点的时间间隔为15分钟,求该地与学校的距离;
(2)若小红出发35分钟后两人相遇,求小红从公园回到学校所用的时间.
分析 (1)分0≤x≤20、20≤x≤30、30≤x≤60三段,利用待定系数法求出y关于x的函数关系式,设该地与学校的距离为s,则第一次经过该地时的时间为5s,第二次经过该地的时间为$\frac{15}{2}$(8-s),根据两次时间间隔为15分钟,即可得出关于s的一元一次方程,解之即可得出结论;
(2)利用一次函数图象上点的坐标特征求出两人相遇时,小红骑行的路程,根据速度=路程÷时间求出小红的速度,再根据时间=4÷速度求出小红到达公园的时间,用60减去该时间,即可求出小红从公园回到学校所用的时间.
解答 解:(1)设小明出发后,y与x之间的函数关系式为y=kx+b,
当0≤x≤20时,将(0,0)、(20,4)代入y=kx+b中,
$\left\{\begin{array}{l}{b=0}\\{20k+b=4}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=0.2}\\{b=0}\end{array}\right.$,
∴y=0.2x;
当20≤x≤30时,y=4;
当30≤x≤60时,将(30,4)、(60,0)代入y=kx+b中,
$\left\{\begin{array}{l}{30k+b=4}\\{60k+b=0}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=-\frac{2}{15}}\\{b=8}\end{array}\right.$,
∴y=-$\frac{2}{15}$x+8.
设该地与学校的距离为s,则第一次经过该地时的时间为5s,第二次经过该地的时间为$\frac{15}{2}$(8-s),
根据题意得:$\frac{15}{2}$(8-s)-5s=15,
解得:s=3.6.
答:如果小明两次经过途中某一地点的时间间隔为15分钟,则该地与学校的距离为3.6千米.
(2)当x=35时,y=-$\frac{2}{15}$x+8=$\frac{10}{3}$,
∴小红从学校去公园的速度为$\frac{10}{3}$÷35=$\frac{2}{21}$,
∴小红到达公园的时间为4÷$\frac{2}{21}$=42(分钟),
∴小红从公园回到学校所用的时间为60-42=18(分钟).
答:若小红出发35分钟后两人相遇,则小红从公园回到学校所用的时间为18分钟.
点评 本题考查了一次函数的应用、一元一次方程的应用以及待定系数法求一次函数解析式,(1)找准等量关系,列出关于s的一元一次方程;(2)根据时间=路程÷速度求出小红到达公园的时间.

 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案| x | … | 1 | 2 | 3 | 4 | 5 | … |
| y | … | 0 | -3 | -6 | -6 | -3 | … |
①$\frac{c}{a}$=6;②函数y=ax2+bx+c的最小值为-6;③抛物线的对称轴是x=$\frac{7}{2}$;④方程ax2+bx+c=0有两个正整数解.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
| A. | 两边分别相等的两直角三角形全等 | |
| B. | 一边相等的两个正三角形全等 | |
| C. | 平行四边形是中心对称图形 | |
| D. | 菱形既是中心对称图形又是轴对称图形 |
 如图,抛物线y=ax2+bx+c的开口向下,与x轴和y轴分别交于点A(-4,0)和点B(0,2),过点B作BC⊥AB交抛物线于点C,连接AC,且∠BAC=∠BAO.
如图,抛物线y=ax2+bx+c的开口向下,与x轴和y轴分别交于点A(-4,0)和点B(0,2),过点B作BC⊥AB交抛物线于点C,连接AC,且∠BAC=∠BAO.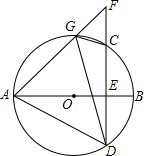 如图,AB是⊙O的直径,弦CD⊥AB于点E,G是弧AC上任意一点,延长AG,与DC的延长线交于点F,连接AD,GD,CG.
如图,AB是⊙O的直径,弦CD⊥AB于点E,G是弧AC上任意一点,延长AG,与DC的延长线交于点F,连接AD,GD,CG.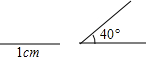 已知一个三角形的两条边长分别是1cm和2cm,一个内角为40°(请在图中标出已知角的度数和已知边的长度,用直尺和圆规作图时,不写作法,保留作图痕迹).
已知一个三角形的两条边长分别是1cm和2cm,一个内角为40°(请在图中标出已知角的度数和已知边的长度,用直尺和圆规作图时,不写作法,保留作图痕迹).