Question

11．如图，E是边长为1的正方形ABCD的对角线BD上一点，且BE=BC，P是CE上任意一点，PQ⊥BC于Q，PR⊥BE于R．求PQ+PR的值．

Answer 1

分析 连接BP，利用面积法求解，PQ+PR的值等于C点到BE的距离，即正方形对角线的一半．

解答 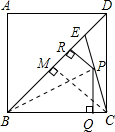解：连接BP，过C作CM⊥BD，如图所示：
∵S_△BCE=S_△BPE+S_△BPC
=$\frac{1}{2}$×BC×PQ×+$\frac{1}{2}$×BE×PR=$\frac{1}{2}$×BC×（PQ+PR）=$\frac{1}{2}$×BE×CM，BC=BE，
∴PQ+PR=CM，
∵BE=BC=1且正方形对角线BD=$\sqrt{2}$BC=$\sqrt{2}$，
又BC=CD，CM⊥BD，
∴M为BD中点，△BDC为直角三角形，
∴CM=$\frac{1}{2}$BD=$\frac{\sqrt{2}}{2}$，
即PQ+PR值是$\frac{\sqrt{2}}{2}$．

点评 本题考查了正方形的性质、三角形面积的计算方法；熟练掌握正方形的性质，并能进行推理计算是解决问题的关键的解题关键．