Question

6．如图1，图2，正方形网格中每个小正方形的边长都是1，每个小格的顶点叫做格点，以格点为顶点分别按下列要求画图．
（1）在图1中，画一个直角三角形，使每条边的长度都是整数．
（2）在图2中，画出一个面积为10的正方形．

Answer 1

分析 （1）由正方形的性质和勾股定理即可得出结果；
（2）正方形的面积得出边长，由勾股定理即可得出结果．

解答 解：（1）∵$\sqrt{{3}^{2}+{4}^{2}}$=5，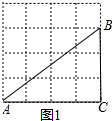
∴两条直角边长为3和4的直角三角形ABC即为所求，
如图1所示：
（2）∵面积为10的正方形的边长为$\sqrt{10}$，
$\sqrt{{1}^{2}+{3}^{2}}$=$\sqrt{10}$，
∴四边形ABCD即为所求，
如图2所示：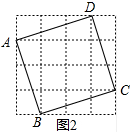

点评 本题考查了正方形的性质、勾股定理；熟练掌握正方形的性质和勾股定理，并能进行推理计算与作图是解决问题的关键．