Question

3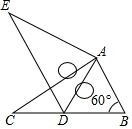．如图，将Rt△ABC绕点A按顺时针旋转一定角度得到Rt△ADE，点B的对应点D恰好落在BC边上．若AB=1，∠B=60°，则CD的长为（　　）

• A． 0.5
• B． 1.5
• C． $\sqrt{2}$
• D． 1

Answer 1

分析 利用含30度的直角三角形三边的关系得到BC=2AB=2，再根据旋转的性质得AD=AB，则可判断△ABD为等边三角形，所以BD=AB=1，然后计算BC-BD即可．

解答 解：∵∠BAC=90°，∠B=60°，
∴BC=2AB=2，
∵Rt△ABC绕点A按顺时针旋转一定角度得到Rt△ADE，点B的对应点D恰好落在BC边上，
∴AD=AB，
而∠B=60°，
∴△ABD为等边三角形，
∴BD=AB=1，
∴CD=BC-BD=2-1=1．
故选D．

点评 本题考查了旋转的性质：对应点到旋转中心的距离相等；对应点与旋转中心所连线段的夹角等于旋转角；旋转前、后的图形全等．