题目内容
在平面直角坐标系中描出下列各点A（5，1），B（5，0），C（2，1），D（2，3），并顺次连接，且将所得图形向下平移4个单位，写出对应点A＇、B＇、C＇、D＇的坐标。
A＇（5，－3）B＇（5，－4）C＇（2，－3）D＇（2，－1）
【解析】试题分析：直接利用平移中点的变化规律求解即可．
试题解析：在平面直角坐标系中各点的位置如图所示：
由点的平移规律可知，点（x，y）向下平移4个单位后的点的坐标是（x，y-4），
∴平移后各点的坐标分别为A′（5，-3），B′（5，-4），C′（2，-3），D′（2，-1）.
练习册系列答案
相关题目
如图，已知线段a、h，作等腰△ABC，使AB＝AC，且BC＝a，BC边上的高AD＝h.张红的作法是：①作线段BC＝a；②作线段BC的垂直平分线MN，MN与BC相交于点D；③在直线MN上截取线段h；④连接AB、AC，则△ABC为所求的等腰三角形．上述作法的四个步骤中，你认为有错误的一步是( )
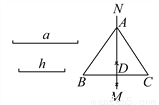
A. ① B. ② C. ③ D. ④
C
【解析】在直线MN上截取线段h，带有随意性，与作图语言的准确性不相符．
故选C． 下列各式能用公式法进行因式分解的是( )
A.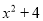 
B. 
C. 
D. 
C
【解析】A选项两项符号相同不能采用公式法因式分解，故本选项错误；B选项中间乘积项不是两底数积的2倍，故本选项错误；C选项符合平方差公式；D选项两项符号相同不能采用公式法因式分解，故本选项错误，
故选C． 观察图象，与图1中的鱼相比，图2中的鱼发生了一些变化．若图1中鱼上点P的坐标为（4，3.2），则这个点在图2中的对应点P1的坐标为__（图中的方格是1×1）．
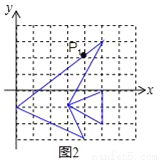
（4，2.2）
【解析】【解析】
由图可知，图1向下平移1个单位，即可得到图2。
∵点P的坐标为（4，3.2），∴点P1的坐标为（4，2.2）．
故答案为：（4，2.2）． 在平面直角坐标系中，将点M（1，2）向左平移2个长度单位后得到点N，则点N的坐标是（ ）
A. （－1，2） B. （3，2） C. （1，4） D. （1，0）
A
【解析】根据坐标的平移变化的规律，左右平移只改变点的横坐标，左减右加。上下平移只改变点的纵坐标，下减上加。因此，
将点M（1，2）向左平移2个长度单位后得到点N的坐标是（1－2，2），即（－1，2）。故选A。 在平面直角坐标系中，点P（-1，2）向右平移3个单位长度得到的点的坐标是 ______ ．
（2，2）．
【解析】试题分析：点P（﹣1，2）向右平移3个单位长度得到的点的坐标是（﹣1+3，2），即（2，2）．故答案为：（2，2）． 已知一元二次方程x2+px+q+1=0的一根为2．
（1）求q关于p的关系式；
（2）求证：抛物线y=x2+px+q与x轴有两个交点；
（1）q= -2p-5；（2）见解析
【解析】试题分析：（1）把x=2代入可求得q与p的关系式；
（2）由△=b2-4ac可判断抛物线与x轴的交点情况.
试题解析：（1）把x=2代入得22+2p+q+1=0，即q= -2p-5；
（2）∵△=p2-4q＞0，
由（1）得△=p2+4（2p+5）=p2+8p+20=（p+4）2+4＞0，
∴一元二次方程x2+px+... 抛物线y=ax2+bx+c（a≠0）与x轴的交点是（-2，0）和（4，0），这条抛物线的对称轴是（ ）
A. 直线x=1 B. 直线x= -1 C. 直线x=2 D. 直线x= -2
A
【解析】∵抛物线y=ax2+bx+c（a≠0）与x轴的交点是（-2，0）和（4，0），
∴这条抛物线的对称轴是：x=，即x=1；
故选：A． 下列图形中，不一定是轴对称图形的是（ ）
A. 等腰三角形 B. 等边三角形 C. 直角三角形 D. 等腰直角三角形
C
【解析】A.等腰三角形是轴对称图形，不符合题意；
B.等边三角形是轴对称图形，不符合题意；
C.直角三角形不一定是轴对称图形，符合题意；
D.等腰直角三角形是轴对称图形，不符合题意.
故选：C.