题目内容
 如图,在平面直角坐标系中,点A的坐标为(2,1).
如图,在平面直角坐标系中,点A的坐标为(2,1).(1)求OA的长.
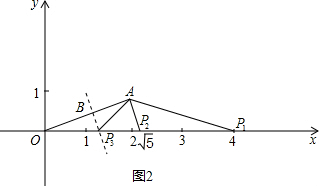
(2)点P为x轴正半轴上的一点,且△AOP是等腰三角形,求点P的坐标.
考点:勾股定理,坐标与图形性质,等腰三角形的性质
专题:
分析:(1)作AE⊥x轴,根据点A的坐标为(2,1),利用勾股定理求出OA的长;
(2)当AO=AP1时,找到P1的位置;当AO=OP2时,找到P2的位置;当OP3=AP3时,找到AP3的位置.
(2)当AO=AP1时,找到P1的位置;当AO=OP2时,找到P2的位置;当OP3=AP3时,找到AP3的位置.
解答: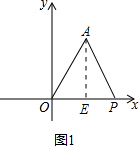 解:(1)如图1,作AE⊥x轴,
解:(1)如图1,作AE⊥x轴,
∵点A的坐标为(2,1),
∴OE=2,AE=1,
∴OA=
=
.
(2)根据等腰三角形的性质可知,P1(4,0),P2(
,0),
设OA解析式为y=kx,
 把(2,1)代入解析式得,
把(2,1)代入解析式得,
1=2k,解得k=
,
则解析式为y=
x,B点坐标为(
,
),即B(1,
).
设BP3解析式为y=-2x+b,把B(1,
)代入解析式得
=-2+b,
解得b=2+
=
,
则解析式为y=-2x+
,
当y=0时,-2x+
=0,解得x=
,P3(
,0).
 解:(1)如图1,作AE⊥x轴,
解:(1)如图1,作AE⊥x轴,∵点A的坐标为(2,1),
∴OE=2,AE=1,
∴OA=
| 22+12 |
| 5 |
(2)根据等腰三角形的性质可知,P1(4,0),P2(
| 5 |
设OA解析式为y=kx,
 把(2,1)代入解析式得,
把(2,1)代入解析式得,1=2k,解得k=
| 1 |
| 2 |
则解析式为y=
| 1 |
| 2 |
| 2+0 |
| 2 |
| 1+0 |
| 2 |
| 1 |
| 2 |
设BP3解析式为y=-2x+b,把B(1,
| 1 |
| 2 |
| 1 |
| 2 |
解得b=2+
| 1 |
| 2 |
| 5 |
| 2 |
则解析式为y=-2x+
| 5 |
| 2 |
当y=0时,-2x+
| 5 |
| 2 |
| 5 |
| 4 |
| 5 |
| 4 |
点评:本题考查了坐标与图形的性质和等腰三角形的性质,熟悉等腰三角形的性质和勾股定理是解题的关键.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
 如图,四边形OABC是矩形,且∠AOx=120°,CO=
如图,四边形OABC是矩形,且∠AOx=120°,CO= 如图,某会展中心在一次会展期间准备在楼梯上铺地毯,已知楼梯的高BC为5m,斜面AC为13m,每一级楼梯宽AD为2m,地毯的价格为每平方米20元,铺完这个楼梯至少需要多少元钱?
如图,某会展中心在一次会展期间准备在楼梯上铺地毯,已知楼梯的高BC为5m,斜面AC为13m,每一级楼梯宽AD为2m,地毯的价格为每平方米20元,铺完这个楼梯至少需要多少元钱?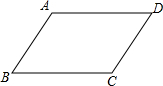 如图,已知?ABCD,求证:∠A=∠C,∠B=∠D(要求:不添加辅助线)
如图,已知?ABCD,求证:∠A=∠C,∠B=∠D(要求:不添加辅助线)
 如图所示,在Rt△ABC中,∠C=90°,∠B=45°,D是BC上一点,∠ADC=60°,BD=10,求CD和AC的长.(结果保留根号)
如图所示,在Rt△ABC中,∠C=90°,∠B=45°,D是BC上一点,∠ADC=60°,BD=10,求CD和AC的长.(结果保留根号) 如图,Rt△ABC和以AB为边的正方形ABEF,已知∠ACB=90°,AC=12,BC=5,求正方形ABEF的面积.
如图,Rt△ABC和以AB为边的正方形ABEF,已知∠ACB=90°,AC=12,BC=5,求正方形ABEF的面积. 如图,平行四边形ABCD的面积为36,对角线AC,BD交于点O点,E为CD上一点,已知四边形EFOG的面积为3,则阴影部分的面积为
如图,平行四边形ABCD的面积为36,对角线AC,BD交于点O点,E为CD上一点,已知四边形EFOG的面积为3,则阴影部分的面积为 如图,已知AB=AC,BC=BD=DA.
如图,已知AB=AC,BC=BD=DA.