题目内容
如图，在数轴上找出表示-
和
的点（要求：尺规作图，不写作法，保留作图痕迹）
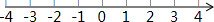
| 5 |
| 10 |
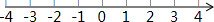
考点：勾股定理,实数与数轴
专题：作图题
分析：因为5=1+4，所以只需作出以1和2为直角边的直角三角形，则其斜边的长即是
．然后以原点为圆心，以
为半径画弧，和数轴的正半轴交于一点即可．根据勾股定理，作出以1和3为直角边的直角三角形，则其斜边的长即是
；再以原点为圆心，以
为半径画弧与数轴的正半轴的交点即为所求；
| 5 |
| 5 |
| 10 |
| 10 |
解答：
解：如图所示，
点E是-
的点，点F是表示
的点．
解：如图所示，点E是-
| 5 |
| 10 |
点评：本题考查的是勾股定理，熟知在任何一个直角三角形中，两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键．
练习册系列答案
相关题目
如图所示，Rt△ABC中，∠C=90°，CA=CB，BD平分∠ABC，DE⊥AB于E．求证：CD=AE．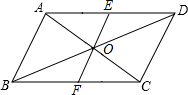
如图，在?ABCD中，AC，BD交于点O，E是AD的中点，EO的延长线交BC于点F．求证：
在△ABC中，AB=AC=25，BC=40，AD为△ABC中BC边上的中线，求AD的长．
如图所示，在Rt△ABC中，∠C=90°，∠B=45°，D是BC上一点，∠ADC=60°，BD=10，求CD和AC的长．（结果保留根号）
如图，?ABCD的对角线AC、BD相交于点O，△AOB是等边三角形，AB=5m．求这个平行四边形的面积．
如图：⊙O1和⊙O2是等圆，P是O1O2的中点．过点P作直线AD交⊙O1于点A、B，交⊙O2于点C、D，求证：AB=CD．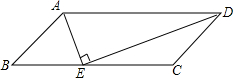
如图，?ABCD中，AE平分∠BAD，交BC于E，DE⊥AE，下列结论：①DE平分∠ADC；②E是BC的中点；③AD=2CD；④梯形ADCE的面积与△ABE的面积比是3：1，其中正确的个数是（ ）
如图，在?ABCD中，CE平分∠BCD交AB于E，DF平分∠ADC交AB于F，若AB=6，BC=4，求EF的长．