题目内容
4.化简下列各式:(1)(-2a+1)(2a+1)-2a(1-2a);
(2)$\frac{x^2}{{{x^2}-1}}÷({\frac{1-2x}{x-1}-x+1})$.
分析 (1)首先计算多项式的乘法以及单项式与多项式的乘法,然后去括号、合并同类项即可;
(2)首先计算括号内的分式,然后把除法转化为乘法,然后进行化简即可.
解答 解:(1)原式=(1-4a2)-(2a-4a2)=1-4a2-2a+4a2=1-2a;
(2)原式=$\frac{{x}^{2}}{(x+1)(x-1)}$÷$\frac{1-2x-(x-1)^{2}}{x-1}$
=$\frac{{x}^{2}}{(x+1)(x-1)}$÷$\frac{-{x}^{2}}{x-1}$
=-$\frac{{x}^{2}}{(x+1)(x-1)}$•$\frac{x-1}{{x}^{2}}$
=-$\frac{1}{x+1}$.
点评 本题主要考查分式的混合运算,通分、因式分解和约分是解答的关键.

练习册系列答案
相关题目
15.下列方程一定是一元二次方程的是( )
| A. | 3x2+$\frac{2}{x}$-1=0 | B. | 5x2-6y-3=0 | C. | ax2-x+2=0 | D. | 3x2=2x |
 若关于x的不等式组的解表示在数轴上如图所示,则这个不等式组的解1<x≤2.
若关于x的不等式组的解表示在数轴上如图所示,则这个不等式组的解1<x≤2.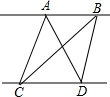 如图,已知AB∥CD,S△ACD=6cm2,则S△BCD=6cm2.
如图,已知AB∥CD,S△ACD=6cm2,则S△BCD=6cm2.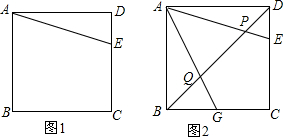
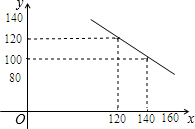 某商店试销一种成本单价为100元/件的运动服,规定试销时的销售单价不低于成本单价,又不高于180元/件,经市场调查,发现销售量y(件)与销售单价x(元)之间的关系满足一次函数y=kx+b(k≠0),其图象如图.
某商店试销一种成本单价为100元/件的运动服,规定试销时的销售单价不低于成本单价,又不高于180元/件,经市场调查,发现销售量y(件)与销售单价x(元)之间的关系满足一次函数y=kx+b(k≠0),其图象如图.