Question

14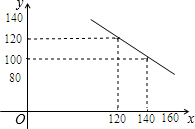．某商店试销一种成本单价为100元/件的运动服，规定试销时的销售单价不低于成本单价，又不高于180元/件，经市场调查，发现销售量y（件）与销售单价x（元）之间的关系满足一次函数y=kx+b（k≠0），其图象如图．
（1）根据图象，求一次函数的解析式；
（2）当销售单价100元≤x≤160元范围内取值时，销售量y不低于80件．（直接填空）

Answer 1

分析 （1）利用图象可得x=120时，y=100；当x=140时，y=100，则可利用待定系数法确定一次函数解析式；
（2）根据（1）中解析式得-x+240≥80，解得x≤160，然后利用销售单价不低于成本单价即可得到销售单价的范围．

解答 解：（1）把（120，120），（140，100）代入y=kx+b得$\left\{\begin{array}{l}{120k+b=120}\\{140k+b=100}\end{array}\right.$，
解得$\left\{\begin{array}{l}{k=-1}\\{b=240}\end{array}\right.$．
所以一次函数的解析式为y=-x+240；
（2）-x+240≥80，解得x≤160，
而100≤x≤180，
所以100元≤x≤160元．
故答案为100元≤x≤160元．

点评 本题考查了一次函数的应用：利用函数图象找出对应值，然后利用待定系数法确定一次函数解析式，然后根据一次函数的性质解决问题．