题目内容
3. 如图,已知△ABC中,∠B=∠C,AB=16厘米,BC=12厘米,点D为AB的中点.如果点P在线段BC上以每秒4厘米的速度由B点向C点运动,同时,点Q在线段CA上以每秒a厘米的速度由C点向A点运动,设运动时间为t(秒)(0≤t≤3).
如图,已知△ABC中,∠B=∠C,AB=16厘米,BC=12厘米,点D为AB的中点.如果点P在线段BC上以每秒4厘米的速度由B点向C点运动,同时,点Q在线段CA上以每秒a厘米的速度由C点向A点运动,设运动时间为t(秒)(0≤t≤3).(1)用的代数式表示PC的长度;
(2)若点P、Q的运动速度相等,经过1秒后,△BPD与△CQP是否全等,请说明理由;
(3)若点P、Q的运动速度不相等,当点Q的运动速度a为多少时,能够使△BPD与△CQP全等?
分析 (1)根据题意、结合图形解答;
(2)分别求出BP、CQ的长,根据全等三角形的判定定理解答;
(3)根据全等三角形的性质求出△BPD与△CQP全等时CQ的长,根据速度公式计算即可.
解答 解:(1)PC=BC-PB=12-4t;
(2)经过1秒后,△BPD与△CQP全等.
∵AB=16,点D为AB的中点,
∴BD=8,
经过1秒后,BP=CQ=4,
∵BC=12,BP=4,
∴CP=8,
∴CP=BD,
在△BPD和△CQP中,
$\left\{\begin{array}{l}{CP=BD}\\{∠C=∠B}\\{CQ=BP}\end{array}\right.$,
∴△BPD≌△CQP;
(3)点P、Q的运动速度不相等时,△BPD与△CQP全等,则CP=BP,
即t=$\frac{6}{4}$=$\frac{3}{2}$秒,
∵AB=16,点D为AB的中点,
∴BD=8,
则CQ=8,
∴点Q的运动速度a=8÷$\frac{3}{2}$=$\frac{16}{3}$,
∴当点Q的运动速度a为$\frac{16}{3}$厘米/秒时,△BPD与△CQP全等.
点评 本题考查的是全等三角形的判定和性质,掌握全等三角形的判定定理、灵活运用分情况讨论思想是解题的关键.

练习册系列答案
相关题目
13.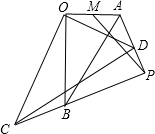 如图,Rt△AOB∽△DOC,∠AOB=∠COD=90°,M为OA的中点,OA=6,OB=8,将△COD绕O点旋转,连接AD,CB交于P点,连接MP,则MP的最大值( )
如图,Rt△AOB∽△DOC,∠AOB=∠COD=90°,M为OA的中点,OA=6,OB=8,将△COD绕O点旋转,连接AD,CB交于P点,连接MP,则MP的最大值( )
 如图,Rt△AOB∽△DOC,∠AOB=∠COD=90°,M为OA的中点,OA=6,OB=8,将△COD绕O点旋转,连接AD,CB交于P点,连接MP,则MP的最大值( )
如图,Rt△AOB∽△DOC,∠AOB=∠COD=90°,M为OA的中点,OA=6,OB=8,将△COD绕O点旋转,连接AD,CB交于P点,连接MP,则MP的最大值( )| A. | 7 | B. | 8 | C. | 9 | D. | 10 |
14.下列方程中是关于x的一元二次方程的是( )
| A. | x2+2x=x2-1 | B. | x3+2x2+3=0 | C. | x(x-1)=1 | D. | 3x2-2xy-5y2=0 |
8.一个多边形的每个内角均为150°,则这个多边形是( )
| A. | 九边形 | B. | 十边形 | C. | 十二边形 | D. | 十五边形 |
13.下列方程中,是一元二次方程的是( )
| A. | x2+$\frac{1}{{x}^{2}}$=0 | B. | ax2+bx+c=0 | C. | (x-1)(x-2)=1 | D. | 3x2-2xy-5y2=0 |
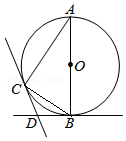 如图,AB是⊙O的直径,BD,CD分别是过⊙O上点B,C的切线,且∠BDC=120°,连接AC.
如图,AB是⊙O的直径,BD,CD分别是过⊙O上点B,C的切线,且∠BDC=120°,连接AC.