题目内容
12.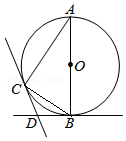 如图,AB是⊙O的直径,BD,CD分别是过⊙O上点B,C的切线,且∠BDC=120°,连接AC.
如图,AB是⊙O的直径,BD,CD分别是过⊙O上点B,C的切线,且∠BDC=120°,连接AC.(1)求∠A的度数;
(2)若点D到BC的距离为2,那么⊙O的半径是多少?
分析 (1)首先连接OC,由BD,CD分别是过⊙O上点B,C的切线,可求得∠BOC的度数,然后由圆周角定理,求得答案;
(2)首先求得∠DCB与∠DBC的度数,然后过点D作DE⊥BC,垂足为E,则DE=2,即可求得BE的长,继而求得BC的长,然后由(1)可知△OBC为等边三角形,即可求得答案.
解答 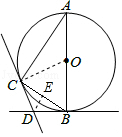 解:(1)连接OC,
解:(1)连接OC,
∵BD,CD分别是过⊙O上点B,C的切线,
∴OC⊥CD,OB⊥BD,
∴∠OCD=∠OBD=90°,
∵∠BDC=120°,
∴∠BOC=360°-∠OCD-∠BDC-∠OBD=60°,
∴∠A=$\frac{1}{2}$∠BOC=30°;
(2)∵BD,CD分别是过⊙O上点B,C的切线,
∴DC=DB,
∴∠DCB=∠DBC=$\frac{1}{2}$(180°-120°)=30°,
过点D作DE⊥BC,垂足为E,则DE=2,
∵∠DBC=30°,
∴BD=2DE=4,
在直角△DEB中,$BE=\sqrt{{4^2}-{2^2}}=2\sqrt{3}$,
∴BC=2BE=$4\sqrt{3}$,
由(1)可知△OBC为等边三角形,
∴OB=BC=$4\sqrt{3}$,
∴⊙O的半径是$4\sqrt{3}$.
点评 此题考查了切线的性质、圆周角定理以及勾股定理等知识.注意准确作出辅助线是解此题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
20.某养殖户的养殖成本逐年增长,第一年的养殖成本为12万元,第3年的养殖成本为16万元.设养殖成本平均每年增长的百分率为x,则下面所列方程中正确的是( )
| A. | 12(1-x)2=16 | B. | 16(1-x)2=12 | C. | 16(1+x)2=12 | D. | 12(1+x)2=16 |
7.下列各选项中的两项是同类项的为( )
| A. | -ab2与-$\frac{1}{2}$a2b | B. | 32与-53 | C. | x2与-y2 | D. | 3xy3与2x2y2 |
4. a,b两数在数轴上的位置如图所示,下列结论中正确的是( )
a,b两数在数轴上的位置如图所示,下列结论中正确的是( )
 a,b两数在数轴上的位置如图所示,下列结论中正确的是( )
a,b两数在数轴上的位置如图所示,下列结论中正确的是( )| A. | a>0,b<0 | B. | a<0,b>0 | C. | ab>0 | D. | 以上均不对 |
1.下列代数式的书写规范的是( )
| A. | m×n | B. | 7ab÷6 | C. | 2$\frac{1}{3}$x | D. | a2-$\frac{1}{a}$ |
 如图,已知△ABC中,∠B=∠C,AB=16厘米,BC=12厘米,点D为AB的中点.如果点P在线段BC上以每秒4厘米的速度由B点向C点运动,同时,点Q在线段CA上以每秒a厘米的速度由C点向A点运动,设运动时间为t(秒)(0≤t≤3).
如图,已知△ABC中,∠B=∠C,AB=16厘米,BC=12厘米,点D为AB的中点.如果点P在线段BC上以每秒4厘米的速度由B点向C点运动,同时,点Q在线段CA上以每秒a厘米的速度由C点向A点运动,设运动时间为t(秒)(0≤t≤3).