题目内容
4．已知实数a、b、c，满足$\frac{（a+b）}{c}=\frac{（b+c）}{a}=\frac{（c+a）}{b}$=k，则k=2．分析 根据等比性质：$\frac{a}{b}$=$\frac{c}{d}$=k⇒$\frac{a+c}{b+d}$=k，可得答案．
解答 解：由等比性质，得
k=$\frac{（a+b）+（b+c）+（c+a）}{c+a+b}$=$\frac{2（a+b+c）}{a+b+c}$=2．
故答案为：2．
点评 本题考查了比例的性质，利用等比性质是解题关键．
练习册系列答案
相关题目
15．下列计算中正确的是（ ）
| A． | （a+b）2=a2+b2 | B． | （a-b）2=a2-b2 | ||
| C． | （2x-y）2=4x2-2xy+y2 | D． | ${（\frac{1}{2}x+5）^2}=\frac{1}{4}{x^2}+5x+25$ |
19．方程x2=x的解为（ ）
| A． | x=0 | B． | x=1 | C． | x1=0，x2=1 | D． | x1=0，x2=-1 |
13．
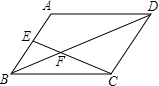如图，在?ABCD中，E是AB的中点，EC交BD于点F，则△BEF与△DCF的面积比为（ ）
如图，在?ABCD中，E是AB的中点，EC交BD于点F，则△BEF与△DCF的面积比为（ ）| A． | $\frac{4}{9}$ | B． | $\frac{1}{9}$ | C． | $\frac{1}{4}$ | D． | $\frac{1}{2}$ |
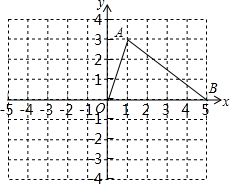如图，网格中每个小正方形的顶点叫格点，△OAB的顶点的坐标分别为O（0，0）、A（1，3）、B（5，0）．