题目内容
9.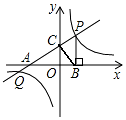 如图,直线y=$\frac{1}{2}$x+3分别交x轴、y轴于点A、C,交双曲线y=$\frac{k}{x}$在第一象限内于点P,过点P作PB⊥x轴于点B,若S△ABC=12.
如图,直线y=$\frac{1}{2}$x+3分别交x轴、y轴于点A、C,交双曲线y=$\frac{k}{x}$在第一象限内于点P,过点P作PB⊥x轴于点B,若S△ABC=12.(1)求A,C两点坐标
(2)求k的值
(3)在第一象限内,当$\frac{1}{2}$x+3≥$\frac{k}{x}$时直接写出x的取值范围.
分析 (1)根据一次函数解析式来求点A、C的坐标;
(2)由三角形的面积公式和(1)中点A、C的坐标易得点P的坐标,将点P的坐标代入反比例函数解析式即可求得k的值;
(3)根据函数图象直接写出答案.
解答  解:(1)直线y=$\frac{1}{2}$x+3交x轴y轴于A、C两点,
解:(1)直线y=$\frac{1}{2}$x+3交x轴y轴于A、C两点,
当y=0,解得:x=-6;
当x=0,解得:y=3,
∴A(-6,0),C(0,3);
(2)∵S△ABC=12,
∵OC=3,
∴AB=8,
∵OA=6,
∴OB=2,且P在第一象限,
∴P(2,4),
由P在反比例函数y=$\frac{k}{x}$上,
故将x=2,y=4代入反比例函数解析式得:4=$\frac{k}{2}$,即k=8;
(3)由图象及点P的横坐标为2,可知:x的范围为x≥2.
点评 此题考查了反比例函数与一次函数的交点,利用待定系数法确定函数解析式,以及一次函数与坐标轴的交点,解决问题的关键是利用数形结合的思想,数形结合思想是数学中重要的思想方法.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
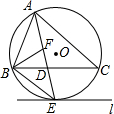 如图,△ABC是⊙O的内接三角形,∠BAC的角平分线AE交⊙O于点E,交BC于点D,过点E作直线l∥BC.
如图,△ABC是⊙O的内接三角形,∠BAC的角平分线AE交⊙O于点E,交BC于点D,过点E作直线l∥BC.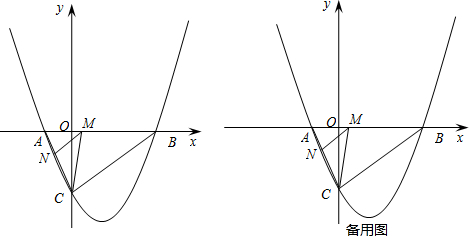
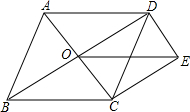 如图,点O是菱形ABCD对角线的交点,DE∥AC,CE∥BD,连接OE.求证:OE=AB.
如图,点O是菱形ABCD对角线的交点,DE∥AC,CE∥BD,连接OE.求证:OE=AB.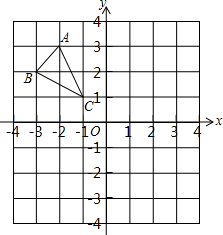 △ABC在平面直角坐标系中的位置如图所示.将△ABC向右平移5个单位后再向下平移3个单位得到△A1B1C1
△ABC在平面直角坐标系中的位置如图所示.将△ABC向右平移5个单位后再向下平移3个单位得到△A1B1C1