题目内容
6.函数正比例函数y=4x与反比例函数y=$\frac{1}{x}$的交点坐标为($\frac{1}{2}$,2)和(-$\frac{1}{2}$,-2).分析 联立解析式可得方程组,可求得交点坐标.
解答 解:联立两函数的解析式得$\left\{\begin{array}{l}{y=4x}\\{y=\frac{1}{x}}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=\frac{1}{2}}\\{y=2}\end{array}\right.$或$\left\{\begin{array}{l}{x=-\frac{1}{2}}\\{y=-2}\end{array}\right.$,
∴交点坐标为($\frac{1}{2}$,2)和(-$\frac{1}{2}$,-2).
故答案为($\frac{1}{2}$,2)和(-$\frac{1}{2}$,-2).
点评 本题主要考查函数的交点坐标,掌握联立解析式求方程组的解是解决这类问题的常用方法.

练习册系列答案
相关题目
 △ABC中,G是△ABC的重心,过G作EF∥AC,求S△BEF:S△ACG.
△ABC中,G是△ABC的重心,过G作EF∥AC,求S△BEF:S△ACG.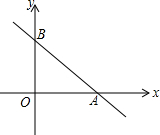 在平面直角坐标系内.已知一次函数y=-x+6的图象与x,y轴分别交于A,B两点,
在平面直角坐标系内.已知一次函数y=-x+6的图象与x,y轴分别交于A,B两点, 如图,玲玲用丝线和印有6行6列方格图的布给她的小猫绣了一个星星图案的饰物.小猫去抓这个饰物时.抓到丝线(阴影部分)的概率是多大?
如图,玲玲用丝线和印有6行6列方格图的布给她的小猫绣了一个星星图案的饰物.小猫去抓这个饰物时.抓到丝线(阴影部分)的概率是多大?