题目内容
14. 如图,已知△ABC≌△DEF,DF∥BC,且∠B=60°,∠F=40°,点A在DE上,则∠BAD的度数为( )
如图,已知△ABC≌△DEF,DF∥BC,且∠B=60°,∠F=40°,点A在DE上,则∠BAD的度数为( )| A. | 15° | B. | 20° | C. | 25° | D. | 30° |
分析 先由△ABC≌△DEF,根据全等三角形的性质得出∠B=∠E=60°,∠C=∠F=40°,由DF∥BC,得出∠1=∠C,等量代换得到∠1=∠F,那么AC∥EF,于是∠2=∠E=60°.由三角形内角和定理求出∠BAC=180°-∠B-∠C=80°,于是∠BAD=∠BAC-∠2=20°.
解答 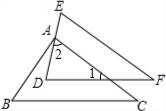 解:∵△ABC≌△DEF,
解:∵△ABC≌△DEF,
∴∠B=∠E=60°,∠C=∠F=40°,
∵DF∥BC,
∴∠1=∠C,
∴∠1=∠F,
∴AC∥EF,
∴∠2=∠E=60°.
∵∠BAC=180°-∠B-∠C=180°-60°-40°=80°,
∴∠BAD=∠BAC-∠2=80°-60°=20°.
故选B.
点评 本题考查了全等三角形的性质,平行线的判定与性质,三角形内角和定理,求出∠2=∠E=60°是解题的关键.

练习册系列答案
相关题目
9. 如图,在△ABC中,∠A=110°,DE∥CB,若∠CDE=140°,则∠B的度数为( )
如图,在△ABC中,∠A=110°,DE∥CB,若∠CDE=140°,则∠B的度数为( )
 如图,在△ABC中,∠A=110°,DE∥CB,若∠CDE=140°,则∠B的度数为( )
如图,在△ABC中,∠A=110°,DE∥CB,若∠CDE=140°,则∠B的度数为( )| A. | 20° | B. | 30° | C. | 35° | D. | 40° |
19.如果物体下降5米记作-5米,则+6米表示( )
| A. | 下降6米 | B. | 上升6米 | C. | 下降或上升6米 | D. | 上升-6米 |
 在?ABCD中,E为对角线BD上一点,且满足∠ECD=∠ACB,AC的延长线与△ABD的外接圆交于点F,证明:∠DFE=∠AFB.
在?ABCD中,E为对角线BD上一点,且满足∠ECD=∠ACB,AC的延长线与△ABD的外接圆交于点F,证明:∠DFE=∠AFB.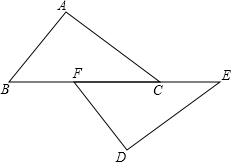 如图,点B、F、C、E在一条直线上,AB=DE,FB=CE,AC=DF,求证:△ABC≌△DEF.
如图,点B、F、C、E在一条直线上,AB=DE,FB=CE,AC=DF,求证:△ABC≌△DEF.