题目内容
4.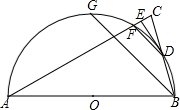 如图,已知△ABC中,AB=AC,∠A=30°,AB=16,以AB为直径的⊙O与BC边相交于点D,与AC交于点F,过点D作DE⊥AC于点E.
如图,已知△ABC中,AB=AC,∠A=30°,AB=16,以AB为直径的⊙O与BC边相交于点D,与AC交于点F,过点D作DE⊥AC于点E.(1)求证:DE是⊙O的切线;
(2)求CE的长;
(3)过点B作BG∥DF,交⊙O于点G,求弧BG的长.
分析 (1)连接AD,OD,则∠ADB=90°,AD⊥BC;又因为AB=AC,所以BD=DC,OA=OB,OD∥AC,易证DE⊥OD,故DE为⊙O的切线;
(2)连接BF,由AB为⊙O的直径,得到∠AFB=90°,根据三角形的中位线的性质得到DE=$\frac{1}{2}$BF,CE=EF,根据直角三角形的性质得到BF=8,根据切割线定理即可得到结论;
(3)连接OG,根据平行线的性质得到∠ABG=∠CDF=30°,根据等腰三角形的性质得到∠OGB=∠OBG=30°,求得∠BOG=120°,根据弧长的公式即可得到结论.
解答 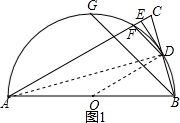 (1)证明:如图1,连接AD,OD;
(1)证明:如图1,连接AD,OD;
∵AB为⊙O的直径,
∴∠ADB=90°,
即AD⊥BC;
∵AB=AC,
∴BD=DC.
∵OA=OB,
∴OD∥AC.
∵DE⊥AC,
∴DE⊥OD.
∴∠ODE=∠DEA=90°,
∴DE为⊙O的切线;
(2)如图,2,连接BF,
∵AB为⊙O的直径,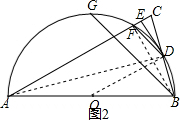
∴∠AFB=90°,
∴BF∥DE,
∵CD=BD,
∴DE=$\frac{1}{2}$BF,CE=EF,
∵∠A=30°AB=16,
∴BF=8,
∴DE=4,
∵DE为⊙O的切线,
∴ED2=EF•AE,
∴42=CE•(16-CE),
∴CE=8-4$\sqrt{3}$,CE=8+4$\sqrt{3}$(不合题意舍去),
(3)如图3,连接OG,
∵∠CFD=∠ABD,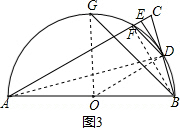
∴∠C=∠CFD=$\frac{180°-∠A}{2}$=75°,
∴∠CDF=30°,
∵BG∥DF,
∴∠ABG=45°,
∵OG=OB,
∴∠OGB=∠OBG=45°,
∴∠BOG=90°,
∴$\widehat{BG}$的长度=$\frac{90•π×8}{180}$=4π.
点评 本题考查了切线的判定和性质,平行线的性质,解直角三角形,圆周角定理,切割线定理,正确的作出辅助线构造直角三角形是解题的关键.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. |  | B. |  | C. |  | D. |  |
 如图,在?ABCD中,AE﹕EB=1﹕2,
如图,在?ABCD中,AE﹕EB=1﹕2, 如图,点P是菱形ABCD的对角线BD上一点,连接CP并延长,交AD于E,交BA的延长线于点F.
如图,点P是菱形ABCD的对角线BD上一点,连接CP并延长,交AD于E,交BA的延长线于点F.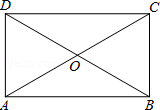 如图,在?ABCD中,对角线AC,BD相交于点O,且OA=OB.
如图,在?ABCD中,对角线AC,BD相交于点O,且OA=OB.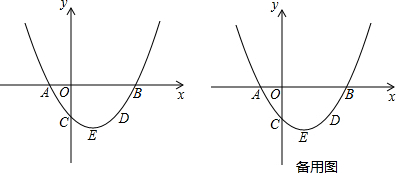
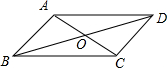 已知?ABCD,边AB=4,AD=8;对角线AC=6,BD=10,则OA=3,BD=5,周长=24.
已知?ABCD,边AB=4,AD=8;对角线AC=6,BD=10,则OA=3,BD=5,周长=24.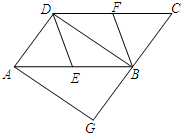 如图,在?ABCD中,E、F分别为边AB、CD的中点,BD是对角线,过点A作AG∥DB,交CB的延长线于点G,∠G=90°.
如图,在?ABCD中,E、F分别为边AB、CD的中点,BD是对角线,过点A作AG∥DB,交CB的延长线于点G,∠G=90°.