题目内容
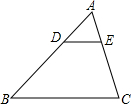如图，△ABC中，DE∥BC，DE分别交边AB，AC于D，E两点，若AD：DB=1：3，则△ADE与四边形BDEC的面积比为考点：相似三角形的判定与性质
专题：
分析：首先证明△ADE∽△ABC，得到△ADE与△ABC的面积之比，问题即可解决．
解答：解：设△ADE与△ABC的面积分别为λ、μ；
∵DE∥BC，
∴△ADE∽△ABC，
∴
=(
)2；
∵
=
，
∴
=
，
∴
=
；
∴△ADE与四边形BDEC的面积比为1：15，
故答案为1：15．
解：设△ADE与△ABC的面积分别为λ、μ；∵DE∥BC，
∴△ADE∽△ABC，
∴
| λ |
| μ |
| AD |
| AB |
∵
| AD |
| DB |
| 1 |
| 3 |
∴
| AD |
| AB |
| 1 |
| 4 |
∴
| λ |
| μ |
| 1 |
| 16 |
∴△ADE与四边形BDEC的面积比为1：15，
故答案为1：15．
点评：该题主要考查了相似三角形的判定及其性质的应用问题；解题的关键是灵活运用有关定理来分析、判断、推理或解答；对综合的分析问题解决问题的能力提出了较高的要求．
练习册系列答案
相关题目
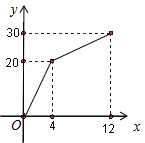有一个安装有进出水管的30升容器，水管每单位时间内进出的水量是一定的，设从某时刻开始的4分钟内只进水不出水，在随后的8分钟内既进水又出水，得到水量y（升）与时间x（分）之间的函数关系如图所示．根据图象信息给出下列说法：
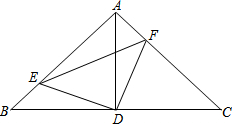如图，在Rt△ABC中，∠BAC=90°，点D为BC中点，点E、F分别为AB、AC上的点，且ED⊥FD．以线段BE、EF、FC为边能否构成一个三角形？若能，请判断此三角形的形状．