题目内容
已知x2+y2-6x+4y+13=0，求2x+3y2．
考点：配方法的应用,非负数的性质：偶次方
专题：
分析：首先把原式分组分解因式，进一步利用非负数的性质求得x、y的数值，进一步代入求得答案即可．
解答：解：∵x2+y2-6x+4y+13=0，
∴（x-3）2+（y+2）2=0，
∴x-3=0，y+2=0，
解得：x=3，y=-2，
∴2x+3y2=18．
∴（x-3）2+（y+2）2=0，
∴x-3=0，y+2=0，
解得：x=3，y=-2，
∴2x+3y2=18．
点评：此题考查因式分解的运用，非负数的性质，以及代数式求值，注意灵活分组，利用完全平方公式解决问题．
练习册系列答案
激活思维优加课堂系列答案
活力试卷系列答案
课课优能力培优100分系列答案
相关题目
如图，在?ABCD中，对角线AC，BD相交于点O，若DO=1.5cm，AB=5cm，BC=4cm，求?ABCD的面积．
如图所示，已知OD平分∠AOC，∠AOB=3∠COD，∠BOC=4∠AOD，则∠AOB的度数为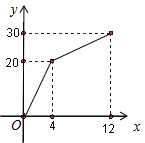
有一个安装有进出水管的30升容器，水管每单位时间内进出的水量是一定的，设从某时刻开始的4分钟内只进水不出水，在随后的8分钟内既进水又出水，得到水量y（升）与时间x（分）之间的函数关系如图所示．根据图象信息给出下列说法：