题目内容
已知二次函数经过A(-1,0),B(2,0),C(0,-3).
(1)求二次函数解析式;
(2)在x轴上求一点Q,使QB与QC的差值最大,并求出这个最大值.
(1)求二次函数解析式;
(2)在x轴上求一点Q,使QB与QC的差值最大,并求出这个最大值.
考点:待定系数法求二次函数解析式,轴对称-最短路线问题
专题:计算题
分析:(1)设二次函数解析式为y=a(x+1)(x-2),把C坐标代入求出a的值,即可确定出解析式;
(2)当QB-QC=BC时,即Q,B重合时,QB-QC最大,求出最大值即可.
(2)当QB-QC=BC时,即Q,B重合时,QB-QC最大,求出最大值即可.
解答:解:(1)设二次函数解析式为y=a(x+1)(x-2),
把(0,-3)代入得:-2a=-3,即a=
,
故二次函数解析式为y=
x2-
x-3;
(2)∵QB-QC<BC,
∴当QB-QC=BC时,即Q,B重合时,QB-QC最大.
Q(2,0),这个最大值=BC=
.
把(0,-3)代入得:-2a=-3,即a=
| 3 |
| 2 |
故二次函数解析式为y=
| 3 |
| 2 |
| 3 |
| 2 |
(2)∵QB-QC<BC,
∴当QB-QC=BC时,即Q,B重合时,QB-QC最大.
Q(2,0),这个最大值=BC=
| 13 |
点评:此题考查了待定系数法求二次函数解析式,熟练掌握待定系数法是解本题的关键.

练习册系列答案
相关题目

 如图所示,已知OD平分∠AOC,∠AOB=3∠COD,∠BOC=4∠AOD,则∠AOB的度数为
如图所示,已知OD平分∠AOC,∠AOB=3∠COD,∠BOC=4∠AOD,则∠AOB的度数为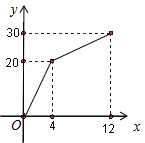 有一个安装有进出水管的30升容器,水管每单位时间内进出的水量是一定的,设从某时刻开始的4分钟内只进水不出水,在随后的8分钟内既进水又出水,得到水量y(升)与时间x(分)之间的函数关系如图所示.根据图象信息给出下列说法:
有一个安装有进出水管的30升容器,水管每单位时间内进出的水量是一定的,设从某时刻开始的4分钟内只进水不出水,在随后的8分钟内既进水又出水,得到水量y(升)与时间x(分)之间的函数关系如图所示.根据图象信息给出下列说法: