题目内容
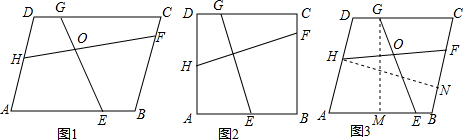
11.问题情境:如图1,在?ABCD中,E、F、G、H分别为AB、BC、CD、DA边上的动点,连接EG、HF,相较于点O,切∠HOE=∠ADC,若AB=a,AD=b,试探究:EG与FH的数量关系,小聪建议分以下三步进行,请你解答:(1)特殊情况,探索结论
当?ABCD是边长为a的正方形(如图2),请写出EG盒FH的数量关系(不必证明);
(2)尝试变题,再探思路
当?ABCD是边长为a的菱形时(如图3)EG与FH又有怎样的数量关系呢?
小聪展示出如下正确的解法(不完整)
如图3,分别过点G、H、作GM⊥AB于点M,HN⊥⊥BC于点N,则∠GME=∠HNF=90°
∵AB×GM=BC×HN,AB=BC
∴GM=HN
…
请补全小聪的解答过程
(3)特例启发,解答题目
猜想:图1中EG与FH的数量关系是$\frac{EG}{FH}=\frac{b}{a}$,并说明理由.
分析 (1)过G作GM⊥AB于M,过H作HN⊥BC于N,求出GM=HN,求出∠GME=∠HNF=90°,∠GEM=∠HFN,证出△GME≌△HNF即可;
(2)过G作GM⊥AB于M,过H作HN⊥BC于N,根据菱形面积公式求出GM=HN,求出∠GME=∠HNF=90°,∠GEM=∠HFN,证出△GME≌△HNF即可;
(3)过G作GM⊥AB于M,过H作HN⊥BC于N,根据平行四边形面积公式求出$\frac{GM}{HN}=\frac{BC}{AB}=\frac{b}{a}$,求出∠GME=∠HNF=90°,∠GEM=∠HFN,证出△GME∽△HNF即可.
解答 (1)解:EG=FH,
理由是:过G作GM⊥AB于M,过H作HN⊥BC于N,如图1: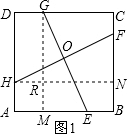
∵四边形ABCD是正方形,
∴DC=AB,AD∥BC,DC∥AB,AD=BC,∠D=∠A=∠B=∠C=90°,
∴GM∥AD∥BC,HN∥DC∥AB,
∴四边形ADGM、四边形GMBC、四边形AHNB,四边形DCNH是平行四边形,
∴DC=HN=AB,AD=GM=BC,
∴HN=GM,
∵∠ADC=∠HOE=90°,
∴∠DHO+∠DGE=360°-90°-90°=180°,
∵AD∥BC,DC∥AB,
∴∠NFH=∠DHF,∠DGE+∠GEM=180°,
∴∠HFN=∠GEM,
∵HN⊥BC,GM⊥AB,
∴∠GME=∠HNF=90°,
在△GME和△HNF中,
$\left\{\begin{array}{l}{∠GEM=∠HFN}\\{∠GME=∠HNF}\\{GM=HN}\end{array}\right.$,
∴△GME≌△HNF(AAS),
∴EG=FH;
(2)EG=FH,理由是:
过G作GM⊥AB于M,过H作HN⊥BC于N,如图2: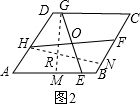
∵四边形ABCD是菱形,
∴DC=AB=BC,AD∥BC,DC∥AB,
∵菱形ABCD的面积S=AB×GM=BC×HN,
∴GM=HN,
∵GM⊥AB,HN⊥BC,
∴∠GME=∠HNF=90°,
∵∠ADC=∠HOE,
∴∠ADC+∠HOG=∠EOH+∠HOG=180°,
∴∠DHO+∠DGE=360°-180°=180°,
∵AD∥BC,DC∥AB,
∴∠NFH=∠DHF,∠DGE+∠GEM=180°,
∴∠HFN=∠GEM,
在△GME和△HNF中,
$\left\{\begin{array}{l}{∠GEM=∠HFN}\\{∠GME=∠HNF}\\{GM=HN}\end{array}\right.$,
∴△GME≌△HNF(AAS),
∴EG=FH.
(3)$\frac{EG}{FH}=\frac{b}{a}$
理由是:
过G作GM⊥AB于M,过H作HN⊥BC于N,如图3: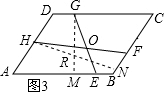
∵四边形ABCD是平行四边形,
∴AD∥BC,DC∥AB,
∵平行四边形ABCD的面积S=AB×GM=BC×HN,
∵AB=a,AD=b,
∴$\frac{GM}{HN}=\frac{b}{a}$,
∵GM⊥AB,HN⊥BC,
∴∠GME=∠HNF=90°,
∵∠ADC=∠HOE,
∴∠ADC+∠HOG=∠EOH+∠HOG=180°,
∴∠DHO+∠DGE=360°-180°=180°,
∵AD∥BC,DC∥AB,
∴∠NFH=∠DHF,∠DGE+∠GEM=180°,
∴∠HFN=∠GEM,
∴△GME∽△HNF,
∴$\frac{EG}{FH}=\frac{GM}{HN}=\frac{b}{a}$,
故答案为:$\frac{EG}{FH}=\frac{b}{a}$.
点评 本题考查了正方形性质,平行四边形性质,菱形性质,面积公式,全等三角形的性质和判定,相似三角形的性质和判定的应用,题目具有一定的代表性,证明过程类似.

 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案| 等级 | 成绩(分) | 频数(人数) | 频率 |
| A | 90~100 | 19 | 0.38 |
| B | 75~89 | 20 | x |
| C | 60~74 | n | y |
| D | 60以下 | 3 | 0.06 |
| 合计 | 50 | 1.00 |
| A. | n=8,x=0.4 | B. | n=8,x=0.16 | C. | n=8,x=0.5 | D. | n=8,x=0.8 |
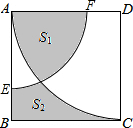 如图,在边长为4的正方形ABCD中,以A为圆心,3为半径作圆弧$\widehat{EF}$,以D为圆心,4为半径作圆弧$\widehat{AC}$.若图中阴影部分的面积分别为S1,S2,则S1-S2=$\frac{25π}{4}$-16.
如图,在边长为4的正方形ABCD中,以A为圆心,3为半径作圆弧$\widehat{EF}$,以D为圆心,4为半径作圆弧$\widehat{AC}$.若图中阴影部分的面积分别为S1,S2,则S1-S2=$\frac{25π}{4}$-16.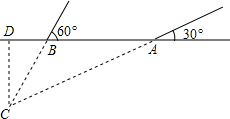 2014年3月,某海域发生航班失联事件,我海事救援部门用高频海洋探测仪进行海上搜救,分别在A、B两个探测点探测到C处是信号发射点,已知A、B两点相距400m,探测线与海平面的夹角分别是30°和60°,若CD的长是点C到海平面的最短距离.
2014年3月,某海域发生航班失联事件,我海事救援部门用高频海洋探测仪进行海上搜救,分别在A、B两个探测点探测到C处是信号发射点,已知A、B两点相距400m,探测线与海平面的夹角分别是30°和60°,若CD的长是点C到海平面的最短距离. 如图,点B(2,2)在双曲线y=$\frac{k}{x}$(x>0)上,点D在双曲线y=-$\frac{3}{x}$(x<0)上,点A、C分别在x轴、y轴的正半轴上,且点A,B,C,D构成的四边形为正方形.
如图,点B(2,2)在双曲线y=$\frac{k}{x}$(x>0)上,点D在双曲线y=-$\frac{3}{x}$(x<0)上,点A、C分别在x轴、y轴的正半轴上,且点A,B,C,D构成的四边形为正方形.
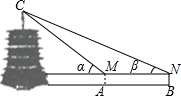 星期天,身高为1.6米的小红、小涛来到一个公园,用他们所学的知识测算一座塔的高度.如图,小红站在A处测得她看塔顶C的仰角α为45°,小涛站在B处测得塔顶C的仰角β为30°,他们又测出A、B两点的距离为41.5米,假设他们的眼睛离头顶都是10厘米,求塔高(结果保留根号).
星期天,身高为1.6米的小红、小涛来到一个公园,用他们所学的知识测算一座塔的高度.如图,小红站在A处测得她看塔顶C的仰角α为45°,小涛站在B处测得塔顶C的仰角β为30°,他们又测出A、B两点的距离为41.5米,假设他们的眼睛离头顶都是10厘米,求塔高(结果保留根号).