题目内容
12.正多边形的一个内角是120度,多边形是几边形?内角和是多少?分析 一个正多边形的每个内角都相等,根据内角与外角互为邻补角,因而就可以求出外角的度数.根据任何多边形的外角和都是360度,利用360除以外角的度数就可以求出外角和中外角的个数,即多边形的边数,根据内角和公式即可求出内角和.
解答 解:外角是180-120=60度,
360÷60=6,则这个多边形是六边形.
内角和为:(6-2)×180°=720°.
点评 考查了多边形内角与外角,根据外角和的大小与多边形的边数无关,由外角和求正多边形的边数,是常见的题目,需要熟练掌握.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案
相关题目
2.已知一个物体由x个相同的正方体堆成,它的主视图和左视图如图所示,那么x的最小值是( )


| A. | 5 | B. | 4 | C. | 3 | D. | 2 |
7.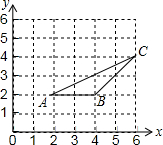 如图,△ABC三个顶点的坐标分别为A(2,2),B(4,2),C(6,4),以原点0为位似中心,将△ABC缩小,使变换后得到的△DEF与△ABC对应边的比为1:2,则线段AC的中点P变换后对应的点的坐标为( )
如图,△ABC三个顶点的坐标分别为A(2,2),B(4,2),C(6,4),以原点0为位似中心,将△ABC缩小,使变换后得到的△DEF与△ABC对应边的比为1:2,则线段AC的中点P变换后对应的点的坐标为( )
 如图,△ABC三个顶点的坐标分别为A(2,2),B(4,2),C(6,4),以原点0为位似中心,将△ABC缩小,使变换后得到的△DEF与△ABC对应边的比为1:2,则线段AC的中点P变换后对应的点的坐标为( )
如图,△ABC三个顶点的坐标分别为A(2,2),B(4,2),C(6,4),以原点0为位似中心,将△ABC缩小,使变换后得到的△DEF与△ABC对应边的比为1:2,则线段AC的中点P变换后对应的点的坐标为( )| A. | (2,$\frac{3}{2}$) | B. | (-2,-$\frac{3}{2}$) | C. | (2,$\frac{3}{2}$)或(-2,-$\frac{3}{2}$) | D. | (8,6)或(-8,-6) |
 如图,在△ABC中,AB>AC,AD是∠BAC的平分线,AD的垂直平分线交BC的延长线于F,交AB、AC于E、G.
如图,在△ABC中,AB>AC,AD是∠BAC的平分线,AD的垂直平分线交BC的延长线于F,交AB、AC于E、G.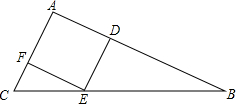 △ABC的边AB=6,AC=4,若菱形DEFA内接于△ABC,则菱形的边长为2.4.
△ABC的边AB=6,AC=4,若菱形DEFA内接于△ABC,则菱形的边长为2.4.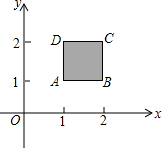 如图,在平面直角坐标系内有一正方形ABCD,其项点坐标分别为A(1,1),B(2,1),C(2,2),D(1,2),要使直线y=-2x+b和此正方形有交点的b的取值范围为3≤x≤6.
如图,在平面直角坐标系内有一正方形ABCD,其项点坐标分别为A(1,1),B(2,1),C(2,2),D(1,2),要使直线y=-2x+b和此正方形有交点的b的取值范围为3≤x≤6. 笑脸(2)是由笑脸(1)经过旋转变换得到的.
笑脸(2)是由笑脸(1)经过旋转变换得到的.