题目内容
1.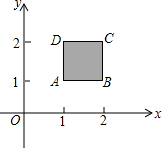 如图,在平面直角坐标系内有一正方形ABCD,其项点坐标分别为A(1,1),B(2,1),C(2,2),D(1,2),要使直线y=-2x+b和此正方形有交点的b的取值范围为3≤x≤6.
如图,在平面直角坐标系内有一正方形ABCD,其项点坐标分别为A(1,1),B(2,1),C(2,2),D(1,2),要使直线y=-2x+b和此正方形有交点的b的取值范围为3≤x≤6.
分析 由于直线y=-2x+b过A点时b最小,过C点时b最大,则把A点和B点坐标代入即可得到b的取值范围.
解答 解:当直线y=-2x+b经过A点(1,1)时,-2+b=1,解得b=3;
当直线y=-2x+b经过C点(2,2)时,-4+b=2,解得b=6,
所以使直线y=-2x+b和正方形有交点的b的取值范围为3≤x≤6.
故答案为3≤x≤6.
点评 本题考查了一次函数图象上点的坐标特征:一次函数y=kx+b,(k≠0,且k,b为常数)的图象是一条直线.它与x轴的交点坐标是(-$\frac{b}{k}$,0);与y轴的交点坐标是(0,b).直线上任意一点的坐标都满足函数关系式y=kx+b.

练习册系列答案
相关题目
6.2009年长春国际动漫艺术节将于2009年5月28日至6月1日在长春市远东艺术馆举行,预计参观人数将超过30万,这个数字用科学记数法表示为( )
| A. | 30×104 | B. | 0.3×106 | C. | 3×105 | D. | 3×104 |
13.下列计算正确的是( )
| A. | (ab)2=ab2 | B. | a2•a3=a6 | C. | a5+a5=2a5 | D. | (a2)3=a5 |
11.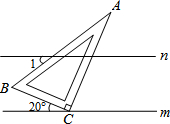 已知:如图,直线m∥n,一把直角三角板ABC(其中∠A=30°)的直角顶点C放在直线m上,边BC与直线m所夹锐角为20°,则∠1的度数为( )
已知:如图,直线m∥n,一把直角三角板ABC(其中∠A=30°)的直角顶点C放在直线m上,边BC与直线m所夹锐角为20°,则∠1的度数为( )
 已知:如图,直线m∥n,一把直角三角板ABC(其中∠A=30°)的直角顶点C放在直线m上,边BC与直线m所夹锐角为20°,则∠1的度数为( )
已知:如图,直线m∥n,一把直角三角板ABC(其中∠A=30°)的直角顶点C放在直线m上,边BC与直线m所夹锐角为20°,则∠1的度数为( )| A. | 30° | B. | 40° | C. | 45° | D. | 60° |