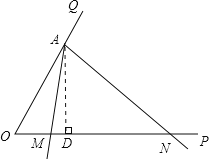
题目内容
【题目】如图,已知A为∠POQ的边OQ上一点,以A为顶点的∠MAN的两边分别交射线OP于M、N两点,且∠MAN=∠POQ=α(α为锐角).当∠MAN以点A为旋转中心,AM边从与AO重合的位置开始,按逆时针方向旋转(∠MAN保持不变)时,设OM=x,ON=y(y>x≥0),△AOM的面积为s,且cosα,OA是方程2z2﹣21z+10=0的两根.
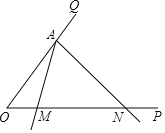
(1)当∠MAN旋转30°时,求点N移动的距离;
(2)求证:AN2=ONMN;
(3)试求y与x的函数关系及自变量的x的取值范围.
【答案】(1)点N移动的距离为10;(2)见解析;(3)y=![]() ,x的取值范围是0≤x<10.
,x的取值范围是0≤x<10.
【解析】
(1)当AM边与AO重合的位置时,△OAN是等边三角形,求此时的ON,当∠MAN旋转30°时,△OAN是直角三角形,解直角三角形求ON,作差即可;(2)根据∠MAN=∠POQ=α,公共角∠MNA=∠ONA,判断△OAN∽△ANM,利用相似比证题;(3)过A作AD⊥OP,垂足为D,解Rt△OAD求AD,OD,在Rt△ADN中,利用勾股定理求x、y的函数关系式.
解:
(1)解方程2z2﹣21z+10=0,得,
z1=![]() ,z2=10,
,z2=10,
∴cosα=![]() ,OA=10,
,OA=10,
∴α=60°,
∵∠MAN=∠POQ=α,当∠MAN以点A为旋转中心,AM边从与AO重合的位置时,△OAN是等边三角形,
ON=OA=10,
当∠MAN旋转30°时,△OAN是直角三角形,
∵OA=10,∠AON=60°,
得ON=20,
故点N移动的距离为10;
(2)∵∠MAN=∠POQ=α,∠MNA=∠ONA,
∴△OAN∽△AMN,
∴![]() ,
,
即AN2=ONMN;
(3)过A作AD⊥OP,垂足为D,在Rt△OAD中,OD=OAcos60°=10×![]() =5,AD=OAsin60°=
=5,AD=OAsin60°=![]() ,
,
∴DN=ON﹣OD=y﹣5,
在Rt△ADN中,AN2=AD2+DN2=75+(y﹣5)2,
又由(2)得AN2=ONMN,即y2﹣10y+100=y(y﹣x),
整理得y=![]() ,
,
∵y>0,
故10﹣x>0,即x<10.
∵x≥0,
∴x的取值范围是0≤x<10.

 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案【题目】某公司从2014年开始投入技术改进资金,经技术改进后,其产品的成本不断降低,具体数据如下表:
年 度 | 2013 | 2014 | 2015 | 2016 |
投入技改资金 | 2.5 | 3 | 4 | 4.5 |
产品成本 | 7.2 | 6 | 4.5 | 4 |
(1)请你认真分析表中数据,从一次函数和反比例函数中确定哪一个函数能表示其变化规律,给出理由,并求出其解析式;
(2)按照这种变化规律,若2017年已投入资金5万元.
①预计生产成本每件比2016年降低多少万元?
②若打算在2017年把每件产品成本降低到3.2万元,则还需要投入技改资金多少万元?(结果精确到0.01万元).