题目内容
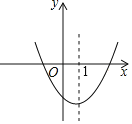
【题目】如图为二次函数y＝ax2+bx+c的图象，在下列说法中：①ac＜0；②方程ax2+bx+c＝0的根是x1，x2，则x1+x2＜0；③a+b+c＞0；④当x＞1时，y随x的增大而增大．正确的说法有_____．（把正确的答案的序号都填在横线上）
【答案】①④．
【解析】
根据抛物线开口方向可判断a的正负，它与y轴的交点位置可判断c的正负，由此可判断①；根据对称轴为直线x=1可判断②；根据图象在x=1处的y值的正负，可判断③；根据图象的对称轴，结合图象的开口方向，则可判断④；由此可得答案.
∵抛物线开口向上、与y轴的交点在x轴的下方，
∴a＞0，c＜0，
∴ac＜0，故①正确；
∵方程ax2+bx+c＝0的根是x1，x2，则对称轴为直线x＝
＝1，
∴x1+x2＝2＞0，故②不正确；
由图象可知当x＝1时，y＜0，
∴a+b+c＜0，故③不正确；
∵抛物线对称轴为直线x＝1，且抛物线开口向上，
∴当x＞1时，y随x的增大而增大，故④正确；
综上可知说法正确的有①④，
故填：①④．
阳光课堂同步练习系列答案【题目】包河区发展农业经济产业，在大圩乡种植多品种的葡萄.已知某葡萄种植户李大爷的葡萄成本为10元
，如果在未来40天葡萄的销售单价
（元）与时间
（天）之间的函数关系式为：
，且葡萄的日销售量
（千克）与时间（天）的关系如下表：
时间 | 1 | 3 | 6 | 10 | 20 | 40 |
日销售量 | 118 | 114 | 108 | 100 | 80 | 40 |
（1）请直接写出与之间的变化规律符合什么函数关系？并求在第15天的日销售量是多少千克？
（2）在后20天（即
），请求出哪一天的日销售利润最大？日销售利润最大为多少？
（3）在实际销售的前20天中，李大爷决定每销售1千克水果就捐赠
元利润（
）给留守贫困儿童作为助学金，前20天销售完后李大爷发现，每天扣除捐赠后的日销售利润随时间
的增大而增大，请求出的取值范围.
【题目】某工厂生产一种合金薄板（其厚度忽略不计），这些薄板的形状均为正方形，边长（单位：cm）在5～50之间，每张薄板的成本价y1（单位：元）与它的边长x（单位：cm）满足关系式y1＝
，每张薄板的出厂价y2（单位：元）由基础价和浮动价两部分组成，其中基础价与薄板的大小无关，是固定不变的，浮动价与薄板的边长x成正比例，在营销过程中得到了表格中的数据．
薄板的边长（cm） | 20 | 30 |
出厂价（元/张） | 50 | 70 |
（1）求一张薄板的出厂价y2与边长x之间满足的函数关系式；
（2）已知：利润＝出厂价﹣成本价
①求一张薄板的利润y与边长x之间满足的函数关系式；
②当边长为多少时，出厂一张薄板获得的利润最大？最大利润是多少？
