��Ŀ����
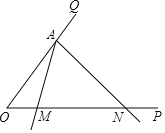
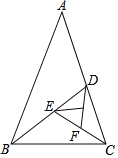
����Ŀ����ͼ��������ABC�У�AB=AC����A=36����������ABC��ƽ����BD��AC�ڵ�D���õ�����BCD����������BCD����BCD��ƽ����CE����BD�ڵ�E���õ�����CDE������������CDE����CDE��ƽ����DF������CE�ڵ�F����������֪AB=b��BC=a������ABCΪ��һ�����������Σ���BCDΪ�ڶ�������������������![]() ��ֵΪ_____����n�����������εĵױ߳�Ϊ_____��������b�Ĵ���ʽ��ʾ��
��ֵΪ_____����n�����������εĵױ߳�Ϊ_____��������b�Ĵ���ʽ��ʾ��
���𰸡�![]()

��������
��֤��ABC�ס�BCD�������BCD���ABC�����Ʊ�Ϊ![]() ������ڶ��������εĵױ߳�Ϊ
������ڶ��������εĵױ߳�Ϊ![]() �������Ƴ������������εĵױ߳�������n�������εĵױ߳����ɣ�
�������Ƴ������������εĵױ߳�������n�������εĵױ߳����ɣ�
�ߡ�A=36�㣬AB=AC��
���ABC=��ACB![]() ��180�㩁36�㣩=72�㣮
��180�㩁36�㣩=72�㣮
��BDƽ�֡�ABC��
���ABD=��CBD![]() ��ABC=36�㣬
��ABC=36�㣬
���BDC=��A+��ABD=72�㣬
��AD=BD=BC����ABC�ס�BCD��
��![]() ��
��
��AB=AC=b��BC=BD=a��
��![]() ��
��
��a2+ab��b2=0��
��a![]() ��ȡ��ֵ����
��ȡ��ֵ����
��![]() ��
��
ͬ����֤����3�����������2�������ε����Ʊ�Ϊ![]() ����3�������εĵױ߳�Ϊ��
����3�������εĵױ߳�Ϊ��![]() ��2b������
��2b������
��n����������ڣ�n��1���������ε����Ʊ�Ϊ![]() ����n�������εĵױ߳�Ϊ��
����n�������εĵױ߳�Ϊ��![]() ����n��1��b��
����n��1��b��
�ʴ�Ϊ��![]() ����
����![]() ����n��1��b��
����n��1��b��

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�