题目内容
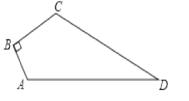
【题目】如图,已知△ABC是面积为4![]() 的等边三角形,△ABC∽△ADE,
的等边三角形,△ABC∽△ADE,
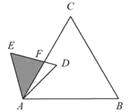
AB=2AD,∠BAD=45°,AC与DE相交于点F,则△AEF的面积
等于___(结果保留根号).
【答案】3-![]()
【解析】
根据相似三角形面积比等于相似比的平方求得三角形ADE的面积,然后求出其边长,过点F作FH⊥AE,过C作CM⊥AB,利用三角函数求出HF的值,即可得出三角形AFE的面积.
解:作CM⊥AB于M,
∵等边△ABC的面积是4![]() ,
,
∴设BM=x,∴tan∠BCM=![]() ,
,
∴BM=![]() CM,
CM,
∴![]() ×CM×AB=
×CM×AB=![]() ×2×
×2×![]() CM2=4
CM2=4![]() ,
,
∴CM=2![]() ,BM=2,
,BM=2,
∴AB=4,AD=![]() AB=2,
AB=2,
在△EAD中,作HF⊥AE交AE于H,

则∠AFH=45°,∠EFH=30°,
∴AH=HF,
设AH=HF=x,则EH=xtan30°=![]() x.
x.
又∵AH+EH=AE=AD=2,
∴x+![]() x=2,
x=2,
解得x=3-![]() .
.
∴S△AEF=![]() ×2×(3-
×2×(3-![]() )=3-
)=3-![]() .
.
故答案为:3-![]()

练习册系列答案
 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
【题目】“姹紫嫣红苗木种植基地”尝试用单价随天数而变化的销售模式销售某种果苗,利用30天时间销售一种成本为10元/株的果苗,售后经过统计得到此果苗,单价在第x天(x为整数)销售的相关信息,如下图表所示:
销售量n(株) |
|
销售单价 m(元/株) | 当1≤x≤20时,m=________ |
当21≤x≤30时, |
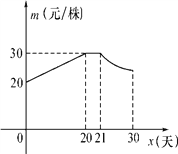
(1)①请将表中当1≤x≤20时,m与x间关系式补充完整;
②计算第几天该果苗单价为25元/株?
(2)求该基地销售这种果苗30天里每天所获利润y(元)关于x(天)的函数关系式;
(3)“吃水不忘挖井人”,为回馈本地居民,基地负责人决定将这30天中,其中获利最多的那天的利润全部捐出,进行“精准扶贫”。试问:基地负责人这次为“精准扶贫”捐赠多少钱?