题目内容
1.已知:x-2的平方根是±2,2x+y+7的立方根是3,则x2+y2的立方根是$\root{3}{100}$.分析 根据题意找出关于x、y的二元一次方程组,解方程组即可得出x、y的值,代入到x2+y2的立方根中即可.
解答 解:根据题意可知有$\left\{\begin{array}{l}{x-2=4}\\{2x+y+7=27}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=6}\\{y=8}\end{array}\right.$,
∴$\root{3}{{x}^{2}+{y}^{2}}$=$\root{3}{36+64}$=$\root{3}{100}$.
故答案为:$\root{3}{100}$.
点评 本题考查了立方根和平方根,解题的关键是根据题意找出关于x、y的二元一次方程组.

练习册系列答案
相关题目
13.烟台是个美丽的城市,两面环海,海岸线长达909000米,数据909000用科学记数法表示为( )
| A. | 90.9×104 | B. | 9.09×106 | C. | 0.909×106 | D. | 9.09×105 |
 如图,在Rt△ABC中,∠A=90°,AB=6,AC=8,D,E分别是边AB,AC的中点,点P从点D出发沿DE方向运动,过点P作PQ⊥BC于Q,过点Q作QR∥BA交AC于R,当点Q与点C重合时,点P停止运动.设BQ=x,QR=y.
如图,在Rt△ABC中,∠A=90°,AB=6,AC=8,D,E分别是边AB,AC的中点,点P从点D出发沿DE方向运动,过点P作PQ⊥BC于Q,过点Q作QR∥BA交AC于R,当点Q与点C重合时,点P停止运动.设BQ=x,QR=y. 如图,面积为20的正方形的一边AB落在数轴上,且点A与原点O重合,则该数轴上一个刻度表示2个单位长度.
如图,面积为20的正方形的一边AB落在数轴上,且点A与原点O重合,则该数轴上一个刻度表示2个单位长度.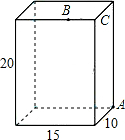 如图,一个无盖的长方体盒子的长为15cm,宽为10cm,高为20cm,点B离点C的距离为
如图,一个无盖的长方体盒子的长为15cm,宽为10cm,高为20cm,点B离点C的距离为