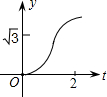题目内容
1.下列计算结果正确的是( )| A. | 2$\sqrt{3}$+4$\sqrt{2}$=6$\sqrt{5}$ | B. | $\sqrt{{(-5)}^{2}}$=-5 | C. | 3$\sqrt{3}$+3$\sqrt{2}$=3$\sqrt{6}$ | D. | $\sqrt{27}$÷$\sqrt{3}$=3 |
分析 根据同类二次根式可判断A、C,根据二次根式的性质判断B,根据二次根式的运算判断D.
解答 解:A、2$\sqrt{3}$、4$\sqrt{2}$不是同类二次根式,不能合并,此选项错误;
B、$\sqrt{(-5)^{2}}$=5,此选项错误;
C、3$\sqrt{3}$、3$\sqrt{2}$不是同类二次根式,不能合并,此选项错误;
D、$\sqrt{27}$$÷\sqrt{3}$=3$\sqrt{3}$÷$\sqrt{3}$=3,此选项正确;
故选:D.
点评 本题主要考查同类二次根式、二次根式的性质、二次根式的运算,熟练掌握二次根式的性质和运算法则是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.下列交通标志中,轴对称图形的个数是( )


| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
6.关于x的分式方程$\frac{2x-a}{x-1}=1$的解为正数,则字母a的取值范围为( )
| A. | a≥1且a≠2 | B. | a>1且a≠2 | C. | a≥1 | D. | a>1 |
13. 如图,⊙O的半径为5,点O到直线l的距离为7,点P是直线l上的一个动点,PQ与⊙O相切于点Q,则PQ的最小值为( )
如图,⊙O的半径为5,点O到直线l的距离为7,点P是直线l上的一个动点,PQ与⊙O相切于点Q,则PQ的最小值为( )
 如图,⊙O的半径为5,点O到直线l的距离为7,点P是直线l上的一个动点,PQ与⊙O相切于点Q,则PQ的最小值为( )
如图,⊙O的半径为5,点O到直线l的距离为7,点P是直线l上的一个动点,PQ与⊙O相切于点Q,则PQ的最小值为( )| A. | $\sqrt{17}$ | B. | $\sqrt{5}$ | C. | 2$\sqrt{6}$ | D. | 2 |
 如图,在△ABC中,∠B=90°,斜边AC的垂直平分线DE与BC的交点是D,连结AD,若AB=6cm,BC=8cm,则DC的长为6.25cm.
如图,在△ABC中,∠B=90°,斜边AC的垂直平分线DE与BC的交点是D,连结AD,若AB=6cm,BC=8cm,则DC的长为6.25cm. 如图,方格纸中每个小正方形的边长都为1,△ABC的顶点均在格点上,在方格纸内将△ABC经过一次平移后得到△A′B′C′,图中标出了点B的对应点B′.利用网格点和三角板画图或计算:
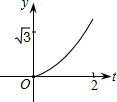
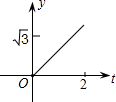
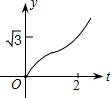
如图,方格纸中每个小正方形的边长都为1,△ABC的顶点均在格点上,在方格纸内将△ABC经过一次平移后得到△A′B′C′,图中标出了点B的对应点B′.利用网格点和三角板画图或计算: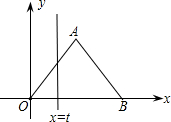 如图,在直角坐标系中,正△AOB的边长为2,设直线x=t(0≤t≤2)截这个三角形所得位于此直线左方的图形的面积为y,则y关于t的函数图象大致是( )
如图,在直角坐标系中,正△AOB的边长为2,设直线x=t(0≤t≤2)截这个三角形所得位于此直线左方的图形的面积为y,则y关于t的函数图象大致是( )