题目内容
 某机械传动装置在静止时如图,连杆PB与点B运动所形成的⊙O交于点A,测得PA=4cm,AB=6cm,⊙O半径为5cm,求点P到圆心O的距离.
某机械传动装置在静止时如图,连杆PB与点B运动所形成的⊙O交于点A,测得PA=4cm,AB=6cm,⊙O半径为5cm,求点P到圆心O的距离.考点:垂径定理的应用,勾股定理
专题:
分析:连接OA,过点O作OD⊥AB于点D,则AD=BD=
AB=3,根据PD=PA+AD可得出PD的长,再根据勾股定理求出OD及OP的长即可.
| 1 |
| 2 |
解答: 解:连接OA,过点O作OD⊥AB于点D,
解:连接OA,过点O作OD⊥AB于点D,
∵AB=6cm,
∴AD=BD=
AB=3,
∴PD=PA+AD=4+3=7.
在Rt△AOD中,
∵OA=5,
∴OD=
=
=4.
在Rt△OPD中,OP=
=
=
.
 解:连接OA,过点O作OD⊥AB于点D,
解:连接OA,过点O作OD⊥AB于点D,∵AB=6cm,
∴AD=BD=
| 1 |
| 2 |
∴PD=PA+AD=4+3=7.
在Rt△AOD中,
∵OA=5,
∴OD=
| OA2-AD2 |
| 52-32 |
在Rt△OPD中,OP=
| OD2+PD2 |
| 42+72 |
| 65 |
点评:本题考查的是垂径定理的应用,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案
相关题目
方程2(x-1)=
的解是( )
| 1 |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
 如图,在Rt△ABC中,∠ACB=90°,∠A=30°,CD是斜边AB上的中线,则图中与CD的长度相等的线段有( )
如图,在Rt△ABC中,∠ACB=90°,∠A=30°,CD是斜边AB上的中线,则图中与CD的长度相等的线段有( )| A、AD与BD |
| B、BD与BC |
| C、AD与BC |
| D、AD、BD与BC |
 已知,如图,在平面直角坐标系内,点A的坐标为(0,12),经过原点的直线l,与经过点A的直线12相交于点B,点B的坐标为(9,3).
已知,如图,在平面直角坐标系内,点A的坐标为(0,12),经过原点的直线l,与经过点A的直线12相交于点B,点B的坐标为(9,3).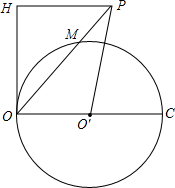 如图,点P为圆O′外一点,OC为圆O′的直径,PO=OC,PO交圆O′于M,OH为圆O′的切线,且PH垂直于OH,若OH=2PM,求tan∠OPO′的值.
如图,点P为圆O′外一点,OC为圆O′的直径,PO=OC,PO交圆O′于M,OH为圆O′的切线,且PH垂直于OH,若OH=2PM,求tan∠OPO′的值. 如图,⊙O是半径为6的正六边形的外接圆,则阴影部分的面积是
如图,⊙O是半径为6的正六边形的外接圆,则阴影部分的面积是 在如图所示的直角坐标系中,解答下列问题:
在如图所示的直角坐标系中,解答下列问题: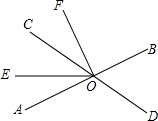 如图,直线AB和CD相交于点O,OE把∠AOC分成两部分且∠AOE:∠EOC=3:5,OF平分∠BOE.
如图,直线AB和CD相交于点O,OE把∠AOC分成两部分且∠AOE:∠EOC=3:5,OF平分∠BOE.