题目内容
解方程:
(1)(x﹣2)2-4=0
(2)x2-4x-5=0
练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
下列各式: 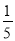 (1?– x),
(1?– x),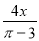 ,
, 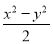 ,
, 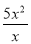 ,其中分式有( )
,其中分式有( )
A. 1个 B. 2个 C. 3个 D. 4个
 A
【解析】是分式;
(1?– x),, 是整式;
故选A.
A
【解析】是分式;
(1?– x),, 是整式;
故选A. 题目内容
解方程:
(1)(x﹣2)2-4=0
(2)x2-4x-5=0
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案下列各式: 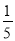 (1?– x),
(1?– x),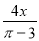 ,
, 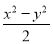 ,
, 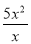 ,其中分式有( )
,其中分式有( )
A. 1个 B. 2个 C. 3个 D. 4个
 A
【解析】是分式;
(1?– x),, 是整式;
故选A.
A
【解析】是分式;
(1?– x),, 是整式;
故选A.