题目内容
下列各式: 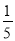 (1?– x),
(1?– x),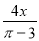 ,
, 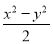 ,
, 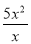 ,其中分式有( )
,其中分式有( )
A. 1个 B. 2个 C. 3个 D. 4个
 A
【解析】是分式;
(1?– x),, 是整式;
故选A.
A
【解析】是分式;
(1?– x),, 是整式;
故选A.
练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
函数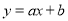 与
与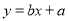 的图象在同一坐标系内的大致( )
的图象在同一坐标系内的大致( )
A. 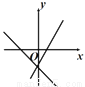 B.
B. 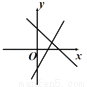 C.
C. 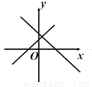 D.
D. 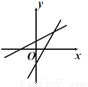
 B
【解析】分四种情况:①当a>0,b>0时,y=ax+b的图象经过第一、二、三象限,y=bx+a的图象经过第一、二、三象限,无选项符合;②当a>0,b<0时,y=ax+b的图象经过第一、三、四象限;y=bx+a的图象经过第一、二、四象限,B选项符合;③当a<0,b>0时,y=ax+b的图象经过第一、二、四象限;y=bx+a的图象经过第一、三、四象限,B选项符合;④当a<0,b<0时,y=a...
B
【解析】分四种情况:①当a>0,b>0时,y=ax+b的图象经过第一、二、三象限,y=bx+a的图象经过第一、二、三象限,无选项符合;②当a>0,b<0时,y=ax+b的图象经过第一、三、四象限;y=bx+a的图象经过第一、二、四象限,B选项符合;③当a<0,b>0时,y=ax+b的图象经过第一、二、四象限;y=bx+a的图象经过第一、三、四象限,B选项符合;④当a<0,b<0时,y=a... 已知x=1时,分式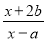 无意义,x=4时分式的值为0,求a+b的值.
无意义,x=4时分式的值为0,求a+b的值.
 -1
【解析】根据当x=1时,分式无意义,可得;根据当x=4时,分式的值为0,可得,即可求出a、b的值,最后代入求值即可.
【解析】
∵x=1时, 无意义,
∴1-a=0,
∴a=1,
∵x=4时, =0,
∴4+2b=0,
∴b=-2,
∴a+b=1+(-2)=-1.
-1
【解析】根据当x=1时,分式无意义,可得;根据当x=4时,分式的值为0,可得,即可求出a、b的值,最后代入求值即可.
【解析】
∵x=1时, 无意义,
∴1-a=0,
∴a=1,
∵x=4时, =0,
∴4+2b=0,
∴b=-2,
∴a+b=1+(-2)=-1. 计算: 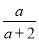 -
-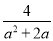 =_____.
=_____.
 【解析】因为-=-=,故答案为: .
【解析】因为-=-=,故答案为: . A,B两地相距48千米,一艘轮船从A地顺流航行至B地,又立即从B地逆流返回A地,共用去9小时.已知水流速度为4千米/时,若设该轮船在静水中的速度为x千米/时,则可列方程( )
A. 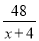 +
+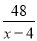 =9 B.
=9 B. 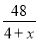 +
+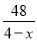 =9
=9
C. 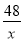 +4=9 D.
+4=9 D. 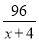 +
+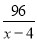 =9
=9
 A
【解析】试题分析:根据题意可以列出相应的方程,从而可以解答本题.由题意可得, .
故选:A.
A
【解析】试题分析:根据题意可以列出相应的方程,从而可以解答本题.由题意可得, .
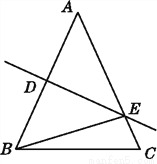
故选:A. 如图,在△ABC中,AB=AC,DE是△ABE的对称轴,△BCE的周长为14,BC=6,求AB的长.
 8
【解析】试题分析:由DE是△ABE的对称轴,根据轴对称的性质可得AE=BE,再由C△BCE=BC+CE+BE=14,可得BC+AC=14,从而求得AB的长.
试题解析:
因为DE是△ABE的对称轴,
所以AE=BE.
所以C△BCE=BC+CE+BE=BC+CE+AE=BC+AC=14.
因为BC=6,所以AC=8.
所以AB=AC=8.
8
【解析】试题分析:由DE是△ABE的对称轴,根据轴对称的性质可得AE=BE,再由C△BCE=BC+CE+BE=14,可得BC+AC=14,从而求得AB的长.
试题解析:
因为DE是△ABE的对称轴,
所以AE=BE.
所以C△BCE=BC+CE+BE=BC+CE+AE=BC+AC=14.
因为BC=6,所以AC=8.
所以AB=AC=8. 已知:如图,在Rt△ABC中,∠ACB=90°,∠A<∠B,CM是斜边AB上的中线,将△ACM沿直线CM折叠,点A落在点D处,如果CD恰好与AB垂直,那么∠A的度数是( )
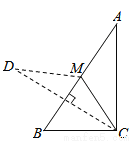
A.30° B.40° C.50° D.60°
 A.
【解析】
试题解析:如图,
∵CM是斜边AB上的中线,
∴CM=AM=AB,
∴∠A=∠MCA(设为α);
由翻折变换的性质得:∠DCM=∠MCA=α;
∵CD⊥AB,
∴∠DCA+∠A=90°,
即3α=90°,
∴∠A=α=30°.
故选A.
A.
【解析】
试题解析:如图,
∵CM是斜边AB上的中线,
∴CM=AM=AB,
∴∠A=∠MCA(设为α);
由翻折变换的性质得:∠DCM=∠MCA=α;
∵CD⊥AB,
∴∠DCA+∠A=90°,
即3α=90°,
∴∠A=α=30°.
故选A. 

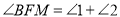 ,求证:
,求证: 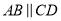 .
.