题目内容
4. 如图,矩形OABC中,AB=1,AO=2,将矩形OABC绕点O按顺时针转90°,得到矩形OA′B′C,则BB′=$\sqrt{10}$.
如图,矩形OABC中,AB=1,AO=2,将矩形OABC绕点O按顺时针转90°,得到矩形OA′B′C,则BB′=$\sqrt{10}$.
分析 延长BC交B′C′于点D,利用旋转的性质以及勾股定理得出答案.
解答  解:如图所示:
解:如图所示:
∵矩形OABC中,AB=1,AO=2,将矩形OABC绕点O按顺时针转90°,得到矩形OA′B′C,
∴BD=3,B′D=1,
则BB′=$\sqrt{B{D}^{2}+B′{D}^{2}}$=$\sqrt{10}$.
故答案为:$\sqrt{10}$.
点评 此题主要考查了矩形的性质以及勾股定理,正确应用勾股定理是解题关键.

练习册系列答案
相关题目
3.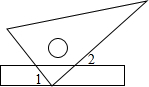 小红把一把直尺与一块三角板如图放置,测得∠1=48°,则∠2的度数为( )
小红把一把直尺与一块三角板如图放置,测得∠1=48°,则∠2的度数为( )
 小红把一把直尺与一块三角板如图放置,测得∠1=48°,则∠2的度数为( )
小红把一把直尺与一块三角板如图放置,测得∠1=48°,则∠2的度数为( )| A. | 38° | B. | 42° | C. | 48° | D. | 52° |
1.二次根式$\sqrt{2x+1}$中x的取值范围是( )
| A. | x≥-$\frac{1}{2}$ | B. | x≥$\frac{1}{2}$ | C. | x>$\frac{1}{2}$ | D. | x>-$\frac{1}{2}$ |
8.有一个不透明的袋子中装有3个红球、1个白球、1个绿球,这些球只是颜色不同.下列事件中属于确定事件的是( )
| A. | 从袋子中摸出1个球,球的颜色是红色 | |
| B. | 从袋子中摸出2个球,它们的颜色相同 | |
| C. | 从袋子中摸出3个球,有颜色相同的球 | |
| D. | 从袋子中摸出4个球,有颜色相同的球 |
16.从1-9这九个自然数中任取一个,是2的倍数的概率是( )
| A. | $\frac{2}{3}$ | B. | $\frac{5}{9}$ | C. | $\frac{4}{9}$ | D. | $\frac{2}{9}$ |
13.若代数式x2-6x+b可化为(x-a)2-1,则b+a的值( )
| A. | 3 | B. | 4 | C. | 11 | D. | 6 |
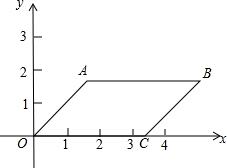 如图,在平行四边形OABC中,已知AB=OC,AB∥OC.A、C两点的坐标分别为$A(\sqrt{3},\sqrt{3}),C(2\sqrt{3},0)$.
如图,在平行四边形OABC中,已知AB=OC,AB∥OC.A、C两点的坐标分别为$A(\sqrt{3},\sqrt{3}),C(2\sqrt{3},0)$.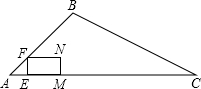 如图,在△ABC中,∠BAC=45°,AB=4$\sqrt{2}$cm,AC=12cm,点E从点A出发沿AC方向以1cm/s的速度运动到点C停止,作EF⊥AC交折线AB-BC于点F,以EF为边向右作矩形EFNM,使EM=2EF.设点E的运动时间为t(s).
如图,在△ABC中,∠BAC=45°,AB=4$\sqrt{2}$cm,AC=12cm,点E从点A出发沿AC方向以1cm/s的速度运动到点C停止,作EF⊥AC交折线AB-BC于点F,以EF为边向右作矩形EFNM,使EM=2EF.设点E的运动时间为t(s). 如图,在△ABC中,AB=AC,∠BAC=90°,点D是BC上一点,DE∥AB,AE∥BC,DE分别交AC、AE于点O和E,连接AD、CE.
如图,在△ABC中,AB=AC,∠BAC=90°,点D是BC上一点,DE∥AB,AE∥BC,DE分别交AC、AE于点O和E,连接AD、CE.