Question

6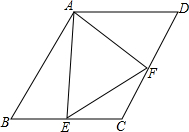．如图，已知菱形ABCD的边长为6cm，∠B=60°，E、F是BC、CD上的两个动点，且∠EAF=60°，试判断四边形AECF的面积是否变化？不变请求值．

Answer 1

分析 先根据菱形的性质得出AB=BC=CD=AD，∠D=∠B=60°，进而求证△ABC、△ACD为等边三角形，得∠4=60°，AC=AB，进而求证△ABE≌△ACF，那么S_△ABE=S_△ACF，然后根据S_{四边形AECF}=S_△AEC+S_△ACF=S_△AEC+S_△ABE=S_△ABC即可解题．

解答 解：四边形AECF的面积不变化．理由如下：
如图，连接AC，
∵四边形ABCD是菱形，
∴AB=BC=CD=AD，∠D=∠B=60°，
∴△ABC、△ACD为等边三角形，
∴∠1+∠2=60°，∠4=60°，AC=AB，
∵∠EAF=∠3+∠2=60°，
∴∠1=∠3．
在△ABE和△ACF中，
$\left\{\begin{array}{l}{∠1=∠3}\\{AB=AC}\\{∠B=∠4}\end{array}\right.$，
∴△ABE≌△ACF（ASA），
∴S_△ABE=S_△ACF，
∴S_{四边形AECF}=S_△AEC+S_△ACF=S_△AEC+S_△ABE=S_△ABC，是定值．
作AH⊥BC于H点，
在直角△ABH中，∵∠B=60°，
∴∠BAH=30°，
∴BH=$\frac{1}{2}$AB=3cm，AH=$\sqrt{3}$BH=3$\sqrt{3}$cm，
∴S_{四边形AECF}=S_△ABC=$\frac{1}{2}$BC•AH=$\frac{1}{2}$×6×3$\sqrt{3}$=9$\sqrt{3}$（cm²）．

点评 本题考查了菱形的性质，全等三角形的判定与性质，含30°角的直角三角形的性质，三角形面积的计算，本题中求证△ABE≌△ACF是解题的关键．