题目内容
15.在RT△ABC中,斜边AB=10,直角边AC=8,以C为圆心,r为半径,若要使⊙C与边AB只有一个公共点,则r的取值范围是r=$\frac{24}{5}$或6<r≤8.分析 因为要使圆与斜边只有一个公共点,所以该圆和斜边相切或和斜边相交,但只有一个交点在斜边上.若d<r,则直线与圆相交;若d=r,则直线于圆相切;若d>r,则直线与圆相离.
解答 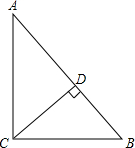 解:如图,∵斜边AB=10,直角边AC=8,
解:如图,∵斜边AB=10,直角边AC=8,
∴BC=$\sqrt{{10}^{2}-{8}^{2}}$=6.
当圆和斜边相切时,则半径即是斜边上的高,r=CD=$\frac{6×8}{10}$=$\frac{24}{5}$;
当圆和斜边相交,且只有一个交点在斜边上时,可以让圆的半径大于短直角边而小于长直角边,则6<r≤8.
故答案为:r=$\frac{24}{5}$或6<r≤8.
点评 本题考查的是直线与圆的位置关系,在解答此题时要注意分两种情况进行讨论,不要漏解.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
3.下列关于x的方程以定是一元一次方程的是( )
| A. | $\frac{2}{x}$-x=1 | B. | (a2+1)x+b=0 | C. | ax2=b | D. | $\sqrt{2x+1}=5$ |
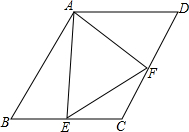 如图,已知菱形ABCD的边长为6cm,∠B=60°,E、F是BC、CD上的两个动点,且∠EAF=60°,试判断四边形AECF的面积是否变化?不变请求值.
如图,已知菱形ABCD的边长为6cm,∠B=60°,E、F是BC、CD上的两个动点,且∠EAF=60°,试判断四边形AECF的面积是否变化?不变请求值.