题目内容
解方程:
(1)(x-2)2=25;
(2)2x2-3x-4=0;
(3)x2-2x=2x+1;
(4)2x2+14x-16=0.
(1)(x-2)2=25;
(2)2x2-3x-4=0;
(3)x2-2x=2x+1;
(4)2x2+14x-16=0.
考点:解一元二次方程-直接开平方法,解一元二次方程-公式法,解一元二次方程-因式分解法
专题:
分析:(1)利用直接开平方法,两边直接开平方即可;
(2)利用公式法,首先计算出△,再利用求根公式进行计算;
(3)首先化为一元二次方程的一般形式,计算出△,再利用求根公式进行计算;
(4)首先根据等式的性质把二次项系数化为1,再利用因式分解法解一元二次方程即可.
(2)利用公式法,首先计算出△,再利用求根公式进行计算;
(3)首先化为一元二次方程的一般形式,计算出△,再利用求根公式进行计算;
(4)首先根据等式的性质把二次项系数化为1,再利用因式分解法解一元二次方程即可.
解答:解:(1)两边直接开平方得:x-2=±5,
x-2=5,x-2=-5,
解得:x1=7,x2=-3;
(2)a=2,b=-3,c=-4,
△=b2-4ac=9+4×2×4=41,
x=
=
,
故x1=
,x2=
;
(3)x2-2x=2x+1,
x2-4x-1=0,
a=1,b=-4,c=-1,
△=b2-4ac=16+4×1×1=20,
x=
=
=2±
,
故x1=2+
,x2=2-
;
(4)2x2+14x-16=0,
x2+7x-8=0,
(x+8)(x-1)=0,
x+8=0,x-1=0,
解得:x1=-8,x2=1.
x-2=5,x-2=-5,
解得:x1=7,x2=-3;
(2)a=2,b=-3,c=-4,
△=b2-4ac=9+4×2×4=41,
x=
-b±
| ||
| 2a |
3±
| ||
| 4 |
故x1=
3+
| ||
| 4 |
3-
| ||
| 4 |
(3)x2-2x=2x+1,
x2-4x-1=0,
a=1,b=-4,c=-1,
△=b2-4ac=16+4×1×1=20,
x=
-b±
| ||
| 2a |
4±2
| ||
| 2 |
| 5 |
故x1=2+
| 5 |
| 5 |
(4)2x2+14x-16=0,
x2+7x-8=0,
(x+8)(x-1)=0,
x+8=0,x-1=0,
解得:x1=-8,x2=1.
点评:此题主要考查了一元二次方程的解法,关键是熟练掌握一元二次方程的解法,并能熟练运用.

练习册系列答案
相关题目
 如图,△ABC中,∠B=45°,∠C=38°,E是BC边上一点,ED交CA的延长线D,交AB于点F,∠D=32°.求∠AFE的大小.
如图,△ABC中,∠B=45°,∠C=38°,E是BC边上一点,ED交CA的延长线D,交AB于点F,∠D=32°.求∠AFE的大小.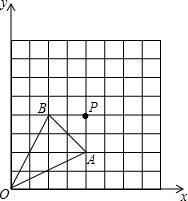 △OAB在坐标系中的位置如图所示.
△OAB在坐标系中的位置如图所示. 如图,△ABC中,AB=AC,AD是△ABC的角平分线,点O为AB的中点,连接DO并延长到点E,使OE=OD,连接AE、BE,求证:四边形AEBD是矩形.
如图,△ABC中,AB=AC,AD是△ABC的角平分线,点O为AB的中点,连接DO并延长到点E,使OE=OD,连接AE、BE,求证:四边形AEBD是矩形. 如图,AB=AC,DE垂直平分AB,且交AB于点D,交AC于点E.已知BC=2,△BCE的周长为6,求△ABC的周长.
如图,AB=AC,DE垂直平分AB,且交AB于点D,交AC于点E.已知BC=2,△BCE的周长为6,求△ABC的周长.