题目内容
12.已知点A(-3,y1),B(2,y2),C(3,y3)在抛物线y=2x2-4x+c上,则y1、y2、y3的大小关系是( )| A. | y1>y2>y3 | B. | y1>y3>y2 | C. | y3>y2>y1 | D. | y2>y3>y1 |
分析 先配方得到抛物线的对称轴为直线x=1,根据二次函数的性质,通过三点与对称轴距离的远近来比较函数值的大小.
解答 解:y=2x2-4x+c=2(x-1)2+c-2,
则抛物线的对称轴为直线x=1,
∵抛物线开口向上,而点B(2,y2)在对称轴上,点A(-3,y1)到对称轴的距离比C(3,y3)远,
∴y1>y3>y2.
故选B.
点评 本题考查了二次函数图象上点的坐标特征:二次函数图象上点的坐标满足其解析式.

练习册系列答案
相关题目
2.下列计算不正确的是( )
| A. | $\sqrt{4}$=±2 | B. | $\sqrt{(-9)^{2}}$=$\sqrt{81}$=9 | ||
| C. | 9的算术平方根是3 | D. | 4的平方根是±2 |
7.已知二次函数y=a(x-1)2+3,当x<1时,y随x的增大而增大,则a取值范围是( )
| A. | a≥0 | B. | a≤0 | C. | a>0 | D. | a<0 |
1.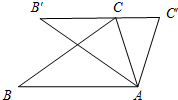 如图,把△ABC绕着点A顺时针方向旋转34°,得到△AB′C′,点C刚好落在边B′C′上.则∠C′=( )
如图,把△ABC绕着点A顺时针方向旋转34°,得到△AB′C′,点C刚好落在边B′C′上.则∠C′=( )
 如图,把△ABC绕着点A顺时针方向旋转34°,得到△AB′C′,点C刚好落在边B′C′上.则∠C′=( )
如图,把△ABC绕着点A顺时针方向旋转34°,得到△AB′C′,点C刚好落在边B′C′上.则∠C′=( )| A. | 56° | B. | 62° | C. | 68° | D. | 73° |
 画出△ABC绕点C顺时针旋转90°后的图象△A′B′C.
画出△ABC绕点C顺时针旋转90°后的图象△A′B′C.