题目内容
2.平面直角坐标系中,点A的坐标为(2,3),把OA绕点O逆时针旋转90°,那么A点旋转后所到点的横坐标是-3.分析 如图,作AB⊥y轴于点B,如图,易得AB=2,OB=3,则把Rt△OAB绕点O逆时针旋转90°得到Rt△OA′B′,根据旋转的性质得∠BOB′=90°,∠ABO=∠A′B′O=90°,OB′=OB=3,即点B′落在x轴的负半轴上,于是得到A点旋转后所到点的横坐标为-3.
解答 解:如图,作AB⊥y轴于点B,如图,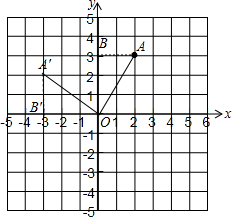
∵点A的坐标为(2,3),
∴AB=2,OB=3,
把△OAB绕点O逆时针旋转90°得到△OA′B′,
∴∠BOB′=90°,∠ABO=∠A′B′O=90°,OB′=OB=3,
∴A点旋转后所到点的横坐标为-3.
故答案为-3.
点评 本题考查了坐标与图形变化-旋转:图形或点旋转之后要结合旋转的角度和图形的特殊性质来求出旋转后的点的坐标.常见的是旋转特殊角度如:30°,45°,60°,90°,180°.解决本题的关键是把线段的旋转转化为直角三角形的旋转.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
12.已知点A(-3,y1),B(2,y2),C(3,y3)在抛物线y=2x2-4x+c上,则y1、y2、y3的大小关系是( )
| A. | y1>y2>y3 | B. | y1>y3>y2 | C. | y3>y2>y1 | D. | y2>y3>y1 |
13.若∠AOB=45°,∠BOC=30°,则∠AOC的度数是( )
| A. | 15° | B. | 30° | C. | 75° | D. | 15°或75° |
11.化简(-x)3•(-x)2的结果正确的是( )
| A. | -x6 | B. | x6 | C. | -x5 | D. | x5 |
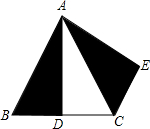 如图,△ABC是等边三角形,D是BC的中点,△ABD经过旋转后达到△ACE的位置,请你思考并回答下列问题:
如图,△ABC是等边三角形,D是BC的中点,△ABD经过旋转后达到△ACE的位置,请你思考并回答下列问题: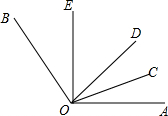 如图所示,OC是∠AOD的平分线,OE是∠BOD的平分线.
如图所示,OC是∠AOD的平分线,OE是∠BOD的平分线.