题目内容
1.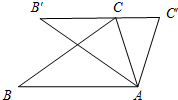 如图,把△ABC绕着点A顺时针方向旋转34°,得到△AB′C′,点C刚好落在边B′C′上.则∠C′=( )
如图,把△ABC绕着点A顺时针方向旋转34°,得到△AB′C′,点C刚好落在边B′C′上.则∠C′=( )| A. | 56° | B. | 62° | C. | 68° | D. | 73° |
分析 利用旋转的性质得出AC=AC′,以及∠CAC′的度数,再利用等腰三角形的性质得出答案.
解答 解:由题意可得:AC=AC′,
∵把△ABC绕着点A顺时针方向旋转34°,得到△AB′C′,点C刚好落在边B′C′上,
∴∠CAC′=34°,
∴∠ACC′=∠C′=$\frac{1}{2}$×(180°-34°)=73°.
故选:D.
点评 此题主要考查了旋转的性质以及等腰三角形的性质等知识,根据题意得出AC=AC′是解题关键.

练习册系列答案
 全程金卷系列答案
全程金卷系列答案
相关题目
12.已知点A(-3,y1),B(2,y2),C(3,y3)在抛物线y=2x2-4x+c上,则y1、y2、y3的大小关系是( )
| A. | y1>y2>y3 | B. | y1>y3>y2 | C. | y3>y2>y1 | D. | y2>y3>y1 |
9.下列各组运算中,结果为负数的是( )
| A. | -(-4) | B. | -|-5| | C. | (-3)×(-2) | D. | (-2)2 |
6.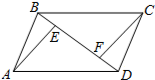 如图,AB∥CD,BC∥AD,AB=CD,BE=DF,图中全等的三角形的对数是( )
如图,AB∥CD,BC∥AD,AB=CD,BE=DF,图中全等的三角形的对数是( )
 如图,AB∥CD,BC∥AD,AB=CD,BE=DF,图中全等的三角形的对数是( )
如图,AB∥CD,BC∥AD,AB=CD,BE=DF,图中全等的三角形的对数是( )| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
13.若∠AOB=45°,∠BOC=30°,则∠AOC的度数是( )
| A. | 15° | B. | 30° | C. | 75° | D. | 15°或75° |
11.化简(-x)3•(-x)2的结果正确的是( )
| A. | -x6 | B. | x6 | C. | -x5 | D. | x5 |