题目内容
9.已知在等腰△ABC中,AB=AC=10,BC=12,正方形DEFG内接于△ABC(D、E、F、G都在△ABC的三边上),则正方形DEFG的边长为$\frac{24}{5}$或$\frac{120}{37}$.分析 应分两种情况进行讨论,作BC边上的高AK和作AB边上高CH进行分析解答,根据相似三角形的性质计算即可.
解答 解:(1)如图1,作BC边上的高AK,交GF于M.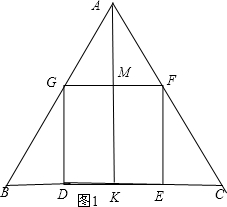
AK=$\sqrt{A{B}^{2}-(\frac{1}{2}BC)^{2}}=\sqrt{1{0}^{2}-{6}^{2}}$=8,
设正方形边长为x,
因为FG∥BC,所以△AGF∽△ABC,
所以GF:BC=AM:AK,
所以x:12=(8-x):8,
所以x=$\frac{24}{5}$,
即正方形边长为$\frac{24}{5}$;
(2)如图2,作AB边上高CH,交EF于N,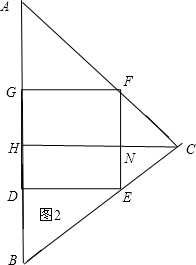
AB•CH=BC•AK,即:10×CH=12×8
所以CH=$\frac{24}{5}$,
因为FEF∥AB,
所以△CEF∽△ABC,
所以x:10=($\frac{24}{5}$-x):$\frac{24}{5}$,
所以x=$\frac{120}{37}$,
即正方形边长为$\frac{120}{37}$.
故答案为:$\frac{24}{5}$;$\frac{120}{37}$.
点评 本题主要考查了相似三角形的判定及性质以及勾股定理的运用,对一道题的分析应考虑全面,不能漏解.

练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
 某研究性学习小组,为了测量某池塘边A、B两点间的距离,让一架航模在直线AB的正上方24米的高度飞行,当航模位于点D处时,在A点处测得航模仰角为60°,5分钟后,当航模在点C处时,在B点测得航模仰角为45°,己知航模飞行的速度为每分钟45米,试计算A、B两点的距离.(结果精确到0.1米,参考数据:$\sqrt{2}=1.41,\sqrt{3}$=1.73.)
某研究性学习小组,为了测量某池塘边A、B两点间的距离,让一架航模在直线AB的正上方24米的高度飞行,当航模位于点D处时,在A点处测得航模仰角为60°,5分钟后,当航模在点C处时,在B点测得航模仰角为45°,己知航模飞行的速度为每分钟45米,试计算A、B两点的距离.(结果精确到0.1米,参考数据:$\sqrt{2}=1.41,\sqrt{3}$=1.73.)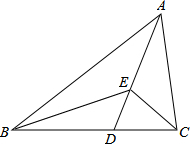 如图,AD是△ABC的角平分线,点E为AD边上一点,且∠BEC=2∠BAC=120°.若BE=2CE,AE=2$\sqrt{3}$,则BC的长为7.
如图,AD是△ABC的角平分线,点E为AD边上一点,且∠BEC=2∠BAC=120°.若BE=2CE,AE=2$\sqrt{3}$,则BC的长为7.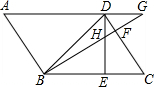 如图,已知平行四边形ABCD中,∠DBC=45°,DE⊥BC于E,BF⊥CD于F,DE、BF相交于H,BF、AD的延长线相交于G,下面结论:(1)AB=BH;(2)∠A=∠BHE;(3)BH=HG;(4)△BHD∽△BDG;(5)DB=$\sqrt{2}$BE.其中正确的结论有(1)(2)(5)(填序号).
如图,已知平行四边形ABCD中,∠DBC=45°,DE⊥BC于E,BF⊥CD于F,DE、BF相交于H,BF、AD的延长线相交于G,下面结论:(1)AB=BH;(2)∠A=∠BHE;(3)BH=HG;(4)△BHD∽△BDG;(5)DB=$\sqrt{2}$BE.其中正确的结论有(1)(2)(5)(填序号).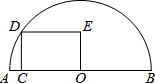 如图,C是半圆O的直径AB上的一个动点(不与A,B重合),过C作AB的垂线交半圆于点D,以点D,C,O为顶点作矩形DCOE.若AB=10,设AC=x,矩形DCOE的面积为y,则下列图象中能表示y与x的函数关系的图象大致是( )
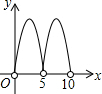
如图,C是半圆O的直径AB上的一个动点(不与A,B重合),过C作AB的垂线交半圆于点D,以点D,C,O为顶点作矩形DCOE.若AB=10,设AC=x,矩形DCOE的面积为y,则下列图象中能表示y与x的函数关系的图象大致是( )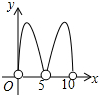
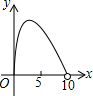
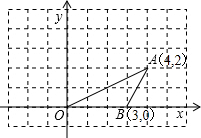 如图,点O、A、B的坐标分别为(0,0)、(4,2)、(3,0),将△OAB绕点O按逆时针方向旋转90°后,得到△OCD.(点A转到点C)
如图,点O、A、B的坐标分别为(0,0)、(4,2)、(3,0),将△OAB绕点O按逆时针方向旋转90°后,得到△OCD.(点A转到点C)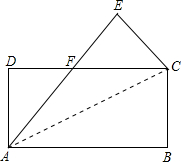 已知:将长方形ABCD沿直线AC对折,将点B折到点E处,AE交CD于点F,
已知:将长方形ABCD沿直线AC对折,将点B折到点E处,AE交CD于点F,