题目内容
18.若使式子$\frac{{\sqrt{1-2x}}}{x}$有意义,则x的取值范围是x≤$\frac{1}{2}$且x≠0.分析 根据当函数表达式是分式时,考虑分式的分母不能为0;当函数表达式是二次根式时,被开方数非负,可得答案..
解答 解:使式子$\frac{{\sqrt{1-2x}}}{x}$有意义,得
$\left\{\begin{array}{l}{1-2x≥0}\\{x≠0}\end{array}\right.$.
解得x≤$\frac{1}{2}$且x≠0,
故答案为:x≤$\frac{1}{2}$且x≠0.
点评 本题考查了二次根式有意义的条件,函数自变量的范围一般从三个方面考虑:当函数表达式是整式时,自变量可取全体实数;当函数表达式是分式时,考虑分式的分母不能为0;当函数表达式是二次根式时,被开方数非负.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
3.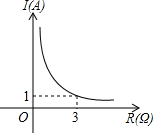 某闭合电路中,电源的电压为定值,电流I(A)与电阻R(Ω)成反比例.如图所示的是该电路中电流I与电阻R之间的函数关系的图象,则用电阻R表示电流I的函数解析式为( )
某闭合电路中,电源的电压为定值,电流I(A)与电阻R(Ω)成反比例.如图所示的是该电路中电流I与电阻R之间的函数关系的图象,则用电阻R表示电流I的函数解析式为( )
 某闭合电路中,电源的电压为定值,电流I(A)与电阻R(Ω)成反比例.如图所示的是该电路中电流I与电阻R之间的函数关系的图象,则用电阻R表示电流I的函数解析式为( )
某闭合电路中,电源的电压为定值,电流I(A)与电阻R(Ω)成反比例.如图所示的是该电路中电流I与电阻R之间的函数关系的图象,则用电阻R表示电流I的函数解析式为( )| A. | $I=\frac{2}{R}$ | B. | $I=\frac{3}{R}$ | C. | $I=\frac{5}{R}$ | D. | $I=\frac{6}{R}$ |
10.在平面直角坐标系中,将直线x=0绕原点顺时针旋转45°,再向上平移1个单位后得到直线a,则直线a对应的函数表达式为( )
| A. | y=x | B. | y=x-1 | C. | y=x+1 | D. | y=-x+1 |
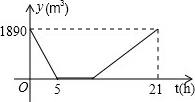 某游泳池内现存水1890立方米,已知该游泳池的防水速度是进水速度的2倍,假设在换水时需要经历“放水→清洗→进水”的过程,其中游泳池内剩余的水量y(m3)与换水时间t(h)之间的函数关系如图所示.试根据图象解答下列问题:
某游泳池内现存水1890立方米,已知该游泳池的防水速度是进水速度的2倍,假设在换水时需要经历“放水→清洗→进水”的过程,其中游泳池内剩余的水量y(m3)与换水时间t(h)之间的函数关系如图所示.试根据图象解答下列问题:



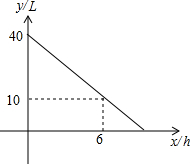 某种拖拉机的油箱可储油40L,加满油并开始工作后,油箱中的余油量y(L)与工作时间x(h)之间为一次函数关系,如图所示.
某种拖拉机的油箱可储油40L,加满油并开始工作后,油箱中的余油量y(L)与工作时间x(h)之间为一次函数关系,如图所示.