题目内容
17．如果双曲线y=$\frac{1}{x}$与直线y=-x+k有两个不同的交点，求k的取值范围．分析 把y=$\frac{1}{x}$代入y=-x+k，整理得到方程x2-kx++=0，则判别式△=k2-4＞0，进而求出k的取值范围．
解答 解：把y=$\frac{1}{x}$代入y=-x+k，
得$\frac{1}{x}$=-x+k，
整理，得x2-kx+1=0，
由题意，得△=k2-4＞0，
解得k＜-2或k＞2．
∴k的取值范围为k＜-2或k＞2．
点评 本题考查了反比例函数与一次函数的交点问题，难度适中，注意当反比例函数与一次函数的图象有交点时，联立它们的解析式整理得到的一元二次方程根的判别式△≥0；无交点时判别式△＜0．
练习册系列答案
名校课堂系列答案
相关题目
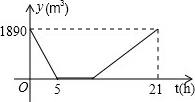某游泳池内现存水1890立方米，已知该游泳池的防水速度是进水速度的2倍，假设在换水时需要经历“放水→清洗→进水”的过程，其中游泳池内剩余的水量y（m3）与换水时间t（h）之间的函数关系如图所示．试根据图象解答下列问题：
12．-3的倒数是（ ）
| A． | 3 | B． | -3 | C． | -$\frac{1}{3}$ | D． | $\frac{1}{3}$ |
2．下列二次根式是最简二次根式的是（ ）
| A． | $\sqrt{0.1}$ | B． | $\sqrt{19}$ | C． | $\sqrt{8}$ | D． | $\sqrt{4\frac{1}{4}}$ |