题目内容
探究:中华人民共和国国旗上的五角星的每个角均相等,小明为了计算每个角的度数,画出了如图①的五角星,每个角均相等,并写出了如下不完整的计算过程,请你将过程补充完整.
解:∵∠AFG=∠C+∠E,∠AGF=∠B+∠D.
∴∠AFG+∠AGF=∠C+∠E+∠B+∠D.
∵∠A+∠AFG+∠AGF=__________°,
∴∠A+∠B+∠C+∠D+∠E=__________°,
∴∠A=∠B=∠C=∠D=∠E=__________°.
拓展:如图②,小明改变了这个五角星的五个角的度数,使它们均不相等,请你帮助小明求∠A、∠B、∠C、∠D、∠E的和.
应用:如图③.小明将图②中的点A落在BE上,点 C落在BD上,若∠B=∠D=36°,则∠CAD+∠ACE+∠E=__________°.
C落在BD上,若∠B=∠D=36°,则∠CAD+∠ACE+∠E=__________°.

【考点】三角形的外角性质;三角形内角和定理.
【专题】探究型.
【分析】根据阅读材料、三角形内角和定理、三角形的外角的性质、结合图形解得即可.
【解答】解:探究:∵∠AFG=∠C+∠E,∠AGF=∠B+∠D.
∴∠AFG+∠AGF=∠C+∠E+∠B+∠D.
∵∠A+∠AFG+∠AGF=180°,
∴∠A+∠B+∠C+∠D+∠E=180°,
∴∠A=∠B=∠C=∠D=∠E=36°;
拓展:∵∠AFG=∠C+∠E,∠AGF=∠B+∠D.
∴∠AFG+∠AGF=∠C+∠E+∠B+∠D.
∵∠A+∠AFG+∠AGF=180°,
∴∠A+∠B+∠C+∠D+∠E=180°;
应用:∠CAD+∠ACE+∠E=180°﹣∠EAD=180°﹣∠B﹣∠D=108°.
【点评】本题考查的是三角形内角和定理、三角形外角的性质,掌握三角形内角和等于180°和三角形的一个外角等于和它不相邻的两个内角的和是解题的关键.

 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案在学习了“25.1.2”概率后,平平和安安两位同学做掷质地均匀的正方体骰子试验,它们共做了120次试验,试验的结果如下表:
| 向上一面的点数 | 1 | 2 | 3 | 4 | 5 | 6 |
| 出现的次数 | 14 | 18 | 12 | 16 | 40 | 20 |
综合上表,平平说:“如果投掷600次,那么向上一面点数是6的次数正好是100次.”安安说:“一次实验中向上一面点数是5的概率最大”.你认为平平和安安的说法中正确的是( )
A.平平 B.安安 C.都正确 D.都错误
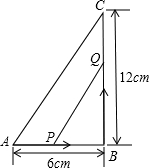
 =160°,∠D=4∠C,求四边形ABCD各内角的度数.
=160°,∠D=4∠C,求四边形ABCD各内角的度数.
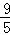 B.
B.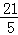 C.
C.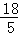 D.
D.