题目内容
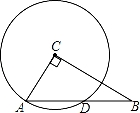
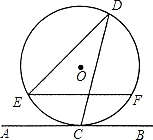
如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,以点C为圆心,CA为半径的圆与AB交于点D,则AD的长为( )
A.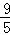 B.
B.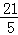 C.
C.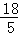 D.
D.
C【考点】垂径定理;勾股定理.
【专题】探究型.
【分析】先根据勾股定理求出AB的长,过C作CM⊥AB,交AB于点M,由垂径定理可知M为AD的中点,由三角形的面积可求出CM的长,在Rt△ACM中,根据勾股定理可求出AM的长,进而可得出结论.
【解答】解:∵在Rt△ABC中,∠ACB=90°,AC=3,BC=4,
∴AB=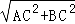 =
=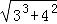 =5,
=5,
过C作CM⊥AB,交AB于点M,如图所示,
∵CM⊥AB,
∴M为AD的中点,
∵S△ABC= AC•BC=
AC•BC= AB•CM,且AC=3,BC=4,AB=5,
AB•CM,且AC=3,BC=4,AB=5,
∴CM=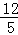 ,
,
在Rt△ACM中,根据勾股定理得:AC2=AM2+CM2,即9=AM2+(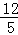 )2,
)2,
解得:AM=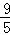 ,
,
∴AD=2AM=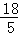 .
.
故选C.

【点评】本题考查的是垂径定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
相关题目
小明记录了一周内每天的最高气温如下表,则这个周内每天最高气温的中位数是( )
| 星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
| 最高气温(℃) |
| 24 | 23 | 25 | 24 | 22 | 21 |
A. 22℃ B. 23℃ C. 24℃  D. 25℃
D. 25℃
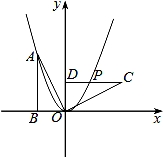
 的开口向__________,对称轴是__________.
的开口向__________,对称轴是__________. C落在BD上,若∠B=∠D=36°,则∠CAD+∠ACE+∠E=__________°.
C落在BD上,若∠B=∠D=36°,则∠CAD+∠ACE+∠E=__________°.
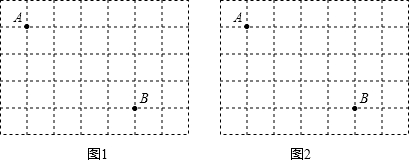
 (2)求证:△ADE是直角三角形;
(2)求证:△ADE是直角三角形;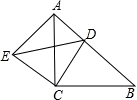
 C.
C.
 22
22