题目内容
17. 如图,AB是⊙O的直径,AC=2,BC=2$\sqrt{3}$,则图中阴影部分的面积为$\frac{4π}{3}$-$\sqrt{3}$.
如图,AB是⊙O的直径,AC=2,BC=2$\sqrt{3}$,则图中阴影部分的面积为$\frac{4π}{3}$-$\sqrt{3}$.
分析 如图,连接OC.图中阴影部分的面积=扇形OBC的面积-△BOC的面积.
解答 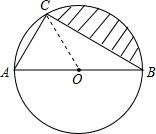 解:如图,连接OC,
解:如图,连接OC,
∵AC=2,BC=2$\sqrt{3}$,
∴tan∠ABC=$\frac{AC}{BC}$=$\frac{\sqrt{3}}{3}$,
∴∠ABC=30°,
∵OB=OC,
∴∠OBC=∠OCB=30°
∴∠BOC=180°-30°-30°=120°,
又∵AB是直径,
∴∠ACB=90°,
∵OC是△ABC斜边上的中线,
∴S△BOC=$\frac{1}{2}$S△ABC=$\frac{1}{2}$×$\frac{1}{2}$AC•BC=$\frac{1}{4}$×2×2$\sqrt{3}$=$\sqrt{3}$,
∴S阴影=S扇形OBC-S△BOC=$\frac{120π×{2}^{2}}{360}$-$\sqrt{3}$=$\frac{4π}{3}$-$\sqrt{3}$,
故答案是:$\frac{4π}{3}$-$\sqrt{3}$.
点评 本题考查了扇形面积的计算、圆周角定理.求图中阴影部分的面积时,采用了“分割法”,即把不规则阴影图形转化为规则图形,然后来计算其面积.

练习册系列答案
 优加精卷系列答案
优加精卷系列答案
相关题目
2.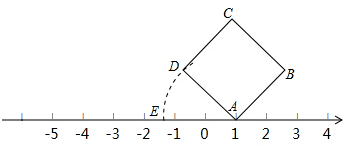 如图,面积为5的正方形ABCD的顶点A在数轴上,且表示的数为1,若AD=AE,则数轴上点E所表示的数为( )
如图,面积为5的正方形ABCD的顶点A在数轴上,且表示的数为1,若AD=AE,则数轴上点E所表示的数为( )
 如图,面积为5的正方形ABCD的顶点A在数轴上,且表示的数为1,若AD=AE,则数轴上点E所表示的数为( )
如图,面积为5的正方形ABCD的顶点A在数轴上,且表示的数为1,若AD=AE,则数轴上点E所表示的数为( )| A. | $-\sqrt{5}$ | B. | $1-\sqrt{5}$ | C. | $\frac{{-1-\sqrt{5}}}{2}$ | D. | $\frac{3}{2}-\sqrt{5}$ |
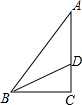 在直角三角形ABC中,BC=6cm,AC=8cm,点D在线段AC上从C向A运动.若设CD=x(m),△ABD的面积为因变量y.
在直角三角形ABC中,BC=6cm,AC=8cm,点D在线段AC上从C向A运动.若设CD=x(m),△ABD的面积为因变量y.

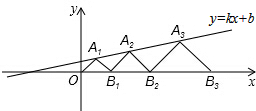 如图,在平面直角坐标系中,点A1、A2、A3…和点B1、B2、B3…分别在直线y=kx+b和x轴上,△OA1B1、△B1A2B2、△B2A3B3…都是等腰直角三角形,如果A1(1,1),A2($\frac{7}{2}$,$\frac{3}{2}$),那么A3的坐标是($\frac{29}{5}$,$\frac{9}{4}$),A2015的坐标是(5×($\frac{3}{2}$)2014-4,($\frac{3}{2}$)2014).
如图,在平面直角坐标系中,点A1、A2、A3…和点B1、B2、B3…分别在直线y=kx+b和x轴上,△OA1B1、△B1A2B2、△B2A3B3…都是等腰直角三角形,如果A1(1,1),A2($\frac{7}{2}$,$\frac{3}{2}$),那么A3的坐标是($\frac{29}{5}$,$\frac{9}{4}$),A2015的坐标是(5×($\frac{3}{2}$)2014-4,($\frac{3}{2}$)2014).