题目内容
15.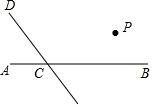 读句画图:如图,直线CD与直线AB相交于C,根据下列语句画图:
读句画图:如图,直线CD与直线AB相交于C,根据下列语句画图:(1)过点P作PQ∥CD,交AB于点Q;
(2)过点P作出点P到直线CD的最短路线,并说明数学道理;
(3)若∠DCB=120°,猜想∠PQC是多少度?并说明理由.
分析 (1)根据平行线的画法画图即可;
(2)利用直角三角板过点P,画垂线即可;
(3)利用平行线的性质结合互余的性质得出答案.
解答  解:(1)如图所示:Q点,即为所求;
解:(1)如图所示:Q点,即为所求;
(2)如图所示:PR,即为所求,
理由:点到直线的距离中,垂线段最短.
(3)∠PQC=60°,
理由:∵PQ∥CD
∴∠DCB+∠PQC=180°,
∵∠DCB=120°,
∴∠PQC=180°-120°=60°.
点评 此题主要考查了基本作图以及垂线的性质,关键是掌握点到直线的距离:直线外一点到直线的垂线段的长度,叫做点到直线的距离.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
20.下列说法正确的是( )
| A. | 两直线被第三条直线相截,同位角相等 | |
| B. | 相等的角是对顶角 | |
| C. | 同旁内角互补,两直线平行 | |
| D. | 互补的两个角一定有一个锐角 |
4.为了响应节能减排的号召,推动绿色生活方式,某品牌汽车4S店准备购进A型和B型两种不同型号的电动汽车共20辆进行销售,这两款电动汽车的成本价和售价如下:
(1)如果该4S店购进20辆电动汽车所花费成本恰好为416万元,那么其中购进A型电动汽车12辆,B型电动汽车8辆;
(2)如果为了保证该4S店将购进的20辆电动汽车全部售出后,所得利润要超过19.3万元,那么A型电动汽车最多购进多少辆?
| 成本价(万元/辆) | 售价(万元/辆) | |
| A型 | 16 | 16.8 |
| B型 | 28 | 29.4 |
(2)如果为了保证该4S店将购进的20辆电动汽车全部售出后,所得利润要超过19.3万元,那么A型电动汽车最多购进多少辆?