题目内容
4.能使得两个直角三角形全等的条件是( )| A. | 一组锐角对应相等 | B. | 两组锐角对应相等 | ||
| C. | 一组边对应相等 | D. | 两组边对应相等 |
分析 直角三角形全等的判定定理有SAS,ASA,AAS,SSS,HL,根据以上定理逐个判断即可.
解答 解:
在Rt△ACB和Rt△DEF中,∠C=∠E=90°,
A、一组锐角对应相等,不符合直角三角形全等的判定定理,不能推理两直角三角形全等,故本选项错误;
B、两组锐角对应相等,不符合直角三角形全等的判定定理,不能推理两直角三角形全等,故本选项错误;
C、一组边对应相等,不符合直角三角形全等的判定定理,不能推理两直角三角形全等,本选项错误;
D、两组边对应相等不符合直角三角形全等的判定定理HL或SAS,能推理两直角三角形全等,故本选项正确;
故选D.
点评 本题考查了全等三角形的判定定理的应用,能熟记全等三角形的判定定理是解此题的关键,注意:直角三角形全等的判定定理有SAS,ASA,AAS,SSS,HL.

练习册系列答案
相关题目
15. 如图所示,小明书上的三角形被墨水污染了,他根据所学知识画出了完全一样的一个三角形,他根据的定理是( )
如图所示,小明书上的三角形被墨水污染了,他根据所学知识画出了完全一样的一个三角形,他根据的定理是( )
 如图所示,小明书上的三角形被墨水污染了,他根据所学知识画出了完全一样的一个三角形,他根据的定理是( )
如图所示,小明书上的三角形被墨水污染了,他根据所学知识画出了完全一样的一个三角形,他根据的定理是( )| A. | SSS | B. | SAS | C. | AAS | D. | ASA |
19.如果a与-3互为倒数,那么a的相反数是( )
| A. | -3 | B. | $-\frac{1}{3}$ | C. | $\frac{1}{3}$ | D. | 3 |
9.在不透明的盒子中装有3个红球,2个白球,它们除颜色外均相同,则从盒中子任意摸出一个球是白球的概率是( )
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
16.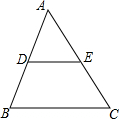 如图,点D、E分别在AB、AC上,以下能推得DE∥BC的条件是( )
如图,点D、E分别在AB、AC上,以下能推得DE∥BC的条件是( )
 如图,点D、E分别在AB、AC上,以下能推得DE∥BC的条件是( )
如图,点D、E分别在AB、AC上,以下能推得DE∥BC的条件是( )| A. | AD:AB=DE:BC | B. | AD:DB=DE:BC | C. | AD:DB=AE:EC | D. | AE:AC=AD:DB |
 如图:在⊙O中,若∠ACB=30°,则∠AOB=60°.
如图:在⊙O中,若∠ACB=30°,则∠AOB=60°.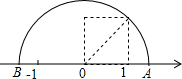 如图,正方形的边长是一个单位长度,则图中A点所表示的数是$\sqrt{2}$,在本题的解答过程,运用了一种重要的数学思想,这种数学思想是数形结合思想.
如图,正方形的边长是一个单位长度,则图中A点所表示的数是$\sqrt{2}$,在本题的解答过程,运用了一种重要的数学思想,这种数学思想是数形结合思想.