题目内容
12.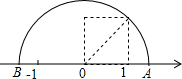 如图,正方形的边长是一个单位长度,则图中A点所表示的数是$\sqrt{2}$,在本题的解答过程,运用了一种重要的数学思想,这种数学思想是数形结合思想.
如图,正方形的边长是一个单位长度,则图中A点所表示的数是$\sqrt{2}$,在本题的解答过程,运用了一种重要的数学思想,这种数学思想是数形结合思想.
分析 根据勾股定理求出正方形的对角线的长,再根据旋转的性质求出A点的数.
解答 解:对角线的长:$\sqrt{{1}^{2}+{1}^{2}}$=$\sqrt{2}$,
根据旋转前后线段的长分别相等,
则A点表示的数=对角线的长=$\sqrt{2}$;
体现了数形结合的思想.
故答案是:$\sqrt{2}$;数形结合.
点评 本题考查了实数与数轴,勾股定理和旋转的性质.旋转变化前后,对应线段、对应角分别相等,图形的大小、形状都不改,要求学生了解常见的数学思想、方法.

练习册系列答案
 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案
相关题目
2. 如图,在△ABC中,AB=AD=DC,∠BAD=20°,则∠C的度数为( )
如图,在△ABC中,AB=AD=DC,∠BAD=20°,则∠C的度数为( )
 如图,在△ABC中,AB=AD=DC,∠BAD=20°,则∠C的度数为( )
如图,在△ABC中,AB=AD=DC,∠BAD=20°,则∠C的度数为( )| A. | 20° | B. | 40° | C. | 60° | D. | 80° |
3.下列各式从左到右的变形是因式分解的是( )
| A. | (a+5)(a-5)=a2-25 | B. | a2-b2=(a+b)(a-b) | ||
| C. | (a+b)2-1=a2+2ab+b2-1 | D. | a2-4a-5=a(a-4)-5 |
17.已知a=2cm,b=10mm,那么$\frac{a}{b}$的值为( )
| A. | $\frac{1}{50}$ | B. | $\frac{1}{5}$ | C. | 2 | D. | $\frac{5}{2}$ |
4.能使得两个直角三角形全等的条件是( )
| A. | 一组锐角对应相等 | B. | 两组锐角对应相等 | ||
| C. | 一组边对应相等 | D. | 两组边对应相等 |
2.下列说法中,正确的是( )
| A. | 正方形是轴对称图形且有四条对称轴 | |
| B. | 平行四边形的对角线垂直平分 | |
| C. | 矩形的对角线互相垂直 | |
| D. | 菱形的对角线相等 |