题目内容

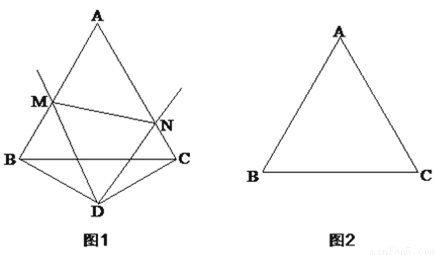
已知：△ABC是边长为3的等边三角形,以BC为底边作一个顶角为120º等腰△BDC.点M、点N分别是AB边与AC边上的点,并且满足∠MDN＝60º.

（1）如图1,当点D在△ABC外部时,求证：BM+CN＝MN；

（2）在（1）的条件下求△AMN的周长；

（3）当点D在△ABC内部时,其它条件不变,请在图2中补全图形,并直接写出△AMN的周长.

（1）证明见解析；（2）6；（3）3. 【解析】试题分析：（1）延长AB至F，使BF=CN，连接DF，只要证明△BDF≌△CND，△DMN≌△DMF即可解决问题； （2）利用（1）中结论即可解决问题； （3）延长BD交AC于P，CD于Q，令KP=QM，交AC于P，连接DK．通过证明△BDQ≌△CDP，△MDQ≌△PDK，△MDN≌△KDN证得△AMN的周长=（AB+AC）=3． ...
练习册系列答案
相关题目

如图，点A为∠α边上任意一点，作AC⊥BC于点C，CD⊥AB于点D，下列用线段比表示cosα的值，错误的是( )

A. B. C. D.

C 【解析】∵AC⊥BC，CD⊥AB， ∴∠α+∠BCD=∠ACD+∠BCD， ∴∠α=∠ACD， ∴cosα=cos∠ACD===， 只有选项C错误. 故选C.

下列方程中，是一元一次方程的是 (　 　)

A. 5x－2y＝9 B. x2－5x＋4＝0 C. ＋3＝0 D. －1＝3

D 【解析】试题解析：A、含有两个未知数，不是一元一次方程； B、未知项的最高次数为2，不是一元一次方程； C、分母中含有未知数，不是一元一次方程； D、符合一元一次方程的定义． 故选D．

分解因式：2x2﹣2=________．

2（x+1）（x﹣1） 【解析】试题分析： 2x2－2 ＝2(x2－1) ＝2(x＋1)(x－1)． 故答案为2(x＋1)(x－1)．

小明在一次射击训练中，共射击10发，成绩如下（单位：环）：8  7  7  8  9  8  7  7  10  8，则中靶8环的频率是（   ）

A. 0.1                                        B. 0.2                                        C. 0.3                                        D. 0.4

D 【解析】试题分析：中靶8环的频数为4，所以中靶8环的频率为＝0.4． 故选D．

如图,已知,点B,E,C,F在一条直线上,AB＝DF,AC＝DE,∠A＝∠D.

(1)求证：AC∥DE；

(2)若BF＝21,EC＝9,求BC的长.

(1)证明见解析；（2）15. 【解析】试题分析：（1）由AB=DF，AC=DE，∠A=∠D，根据SAS即可证明； （2）由△ABC≌△DFE，推出BC=EF，推出BE=CF，由BF=21，EC=9，推出BE+CF=12，可得BE=CF=6，由此即可解决问题. 试题解析：（1）证明：在△ABC和△DFE中， ， ∴△ABC≌△DFE（SAS）， ∴∠ACB=∠D...

当x=2016时,分式的值＝___________.

2013 【解析】试题解析：当x=2016时，分式=x-3， 则原式=2016-3=2013． 故答案为：2013．

解方程： ．

x=-38 【解析】试题分析： 这是一道解一元一次方程的题，按解一元一次方程的一般步骤解答即可. 试题解析： 去分母得：15x-3（x-2）=5（2x-5）-3×15， 去括号得：15x-3x+6=10x-25-45， 移项得： ， 合并同类项得： ， 系数化为1得：x=-38．

二次函数y=ax2+bx+c的图象如图所示，对称轴是直线x=﹣1，有以下结论：①abc＞0；②4ac＜b2；③2a+b=0；④a﹣b+c＞2．其中正确的结论的个数是（　　）

A. 1 B. 2 C. 3 D. 4

C 【解析】①∵抛物线开口向下，∴a＜0，∵抛物线的对称轴为直线x==﹣1，∴b=2a＜0，∵抛物线与y轴的交点在x轴上方，∴c＞0，∴abc＞0，所以①正确； ②∵抛物线与x轴有2个交点，∴△=b2-4ac＞0，∴4ac