题目内容
19.某商店销售一种工艺品,成本价是50元/件,经过调查,得到如表中的数据:| 销售单价x(元/件) | … | 70 | 80 | 90 | 100 | … |
| 每天销售量(y件) | … | 100 | 90 | 80 | 70 | … |
(2)当销售单价定为多少时,销售该工艺品每天获得的利润最大?最大利润是多少?
分析 (1)根据表格中的数据可知,当x的值每增加10时,对应y的值每次减少10,故可模拟成一次函数,由待定系数法可求得解析式;
(2)根据:总利润=单件利润×销售量可得函数关系式,配方成顶点式可知其最大值.
解答 解:(1)设这个一次函数为y=kx+b(k≠0),
∵这个一次函数的图象经过(70,100)、(80,90)这两点,
∴$\left\{\begin{array}{l}{70k+b=100}\\{80k+b=90}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-1}\\{b=170}\end{array}\right.$,
∴销售量y与销售单价x的函数关系式是y=-x+170.
(2)设每天获得的利润是W元,依题意得:
W=(x-50)(-x+170)=-x2+220x-8500=-(x-110)2+3600,
∴当x=110时,W有最大值3600.
∴当销售单价是100元时,每天获得的利润最大,最大利润是3600元.
点评 本题主要考查二次函数的实际应用能力,待定系数法求一次函数解析式是根本,找到等量关系并列出二次函数关系式是关键.

练习册系列答案
相关题目
10.下列说法中错误的是( )
| A. | 了解一批电视机的使用寿命,适合用抽样调查的方式 | |
| B. | 掷一枚均匀的骰子,骰子停止转动后6点朝上是必然事件 | |
| C. | 若a为实数,则|a|<0是不可能事件 | |
| D. | 甲、乙两人各进行10次射击,两人射击成绩的方差分别为S甲2=2,S乙2=4,则甲射击成绩更稳定 |
4.下列运算中,正确的是( )
| A. | 3x+2x2=5x2 | B. | 2a2b-a2b=1 | C. | (-6)+(-2)=-3 | D. | (-$\frac{2}{3}$)2=$\frac{4}{9}$ |
11.下列因式分解中,正确的个数为( )
①x3+2xy+x=x(x2+2y);
②x2+4x+4=(x+2)2;
③-x2+y2=(x+y)(x-y);
④ax2-7ax+6a=a(x-1)(x-6);
⑤-2x2y+12xy-18y=-2y(x-3)2.
①x3+2xy+x=x(x2+2y);
②x2+4x+4=(x+2)2;
③-x2+y2=(x+y)(x-y);
④ax2-7ax+6a=a(x-1)(x-6);
⑤-2x2y+12xy-18y=-2y(x-3)2.
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
9.阅读:在直线上有n个不同的点,则此图中共有多少条线段?通过分析、画图尝试得如下表格:
问题:
(1)把表格补充完整;
(2)根据上述得到的信息解决下列问题:
①某学校七年级共有20个班进行辩论赛,规定进行单循环赛(每两班赛一场),那么该校七年级的辩论赛共要进行多少场?
②乘火车从A站出发,沿途经过10个车站方可到达B站,那么在A,B两站之间需要安排多少种不同的车票?
| 图形 | 直线上点的个数 | 共有线段的条数 | 两者关系 |
 | 2 | 1 | 0+1=$\frac{2×(2-1)}{2}$=1 |
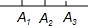 | 3 | 3 | 0+1+2=$\frac{3×(3-1)}{2}$=3 |
 | 4 | 6 | 0+1+2+3=$\frac{4×(4-1)}{2}$=6 |
| … | … | … | … |
 | n |
(1)把表格补充完整;
(2)根据上述得到的信息解决下列问题:
①某学校七年级共有20个班进行辩论赛,规定进行单循环赛(每两班赛一场),那么该校七年级的辩论赛共要进行多少场?
②乘火车从A站出发,沿途经过10个车站方可到达B站,那么在A,B两站之间需要安排多少种不同的车票?
 如图,已知点B在线段AC上,点E在线段BD上,∠ABD=∠DBC,AB=DB,EB=CB,M,N分别是AE,CD的中点,现有如下结论:①∠ABD=∠BDN;②MB=NB;③MB⊥NB;④S△ABM=S△BCN,其中正确的结论是②③④(只填序号).
如图,已知点B在线段AC上,点E在线段BD上,∠ABD=∠DBC,AB=DB,EB=CB,M,N分别是AE,CD的中点,现有如下结论:①∠ABD=∠BDN;②MB=NB;③MB⊥NB;④S△ABM=S△BCN,其中正确的结论是②③④(只填序号). 数a,b,c在数轴上的位置如图所示,化简式子|a-b|-|b-c|-|a+c|-|b|+2|a|.
数a,b,c在数轴上的位置如图所示,化简式子|a-b|-|b-c|-|a+c|-|b|+2|a|.